| [HomePage] | Prof Morris Kline | |
CHAPTER 7 Mathematics for Mathematics' Sake
"One may say that mathematics talks about things which are of no concern at all to man. ...It seems an irony of creation that man's mind knows how to handle things the better the farther removed they are from the center of his existence. Thus we are cleverest where knowledge matters least: in mathematics, especially in number theory."
Hermann Weyl
The new mathematics presents the subject as self-sufficient. Presumably mathematics can feed on itself to grow and offers values when studied in and for itself.
For example, mathematics is presented as self-generating. Thus, granted the whole numbers, the fractions can be and are introduced in the new curricula by asking for some number x that solves 3x = 7. Clearly no whole number will do and therefore, so the story goes, mathematicians are led to introduce fractions such as 7/3.
Given the positive whole numbers and fractions one asks what number x satisfies the equation x + 5 = 2. Again the existing numbers are found to be useless for solving such equations and so negative numbers are created. The same approach motivates the introduction of irrational numbers and complex numbers, that is, numbers involving the square root of negative numbers, for example, \/-5.
Not only are the various types of numbers introduced by raising mathematical questions, but the axioms that hold for the whole numbers are assumed to apply to each new class introduced and thereby one proves properties of each of these classes. We have illustrated this latter fact in connection with the deductive approach adopted by the new mathematics.
The introduction of new mathematical ideas by raising questions about old ones is illustrated by another situation. Having solved linear equations, that is, equations of the form ax + b = 0, it is mathematically relevant to ask whether one can solve equations such as x2 + 7x + 9 = 0, x2 - 5x + 4 = 0, and more generally ax2 + bx + c = 0.
Not all of mathematics can be arrived at by raising questions about ideas already studied. Geometry must be introduced afresh. However, once this subject is launched, it is easy to raise mathematical questions that lead to new geometrical topics. For example, after students have studied congruent triangles one can ask, "What can be said about two triangles for which the angles of one equal the angles of the other?" Such tri-angles need not be congruent but they are similar, and thus the study of similar triangles is suggested. Again, having considered triangles, which are three-sided figures, one can raise and answer question about four-sided figures or quadrilaterals. These examples may serve to illustrate what is meant by mathematics being self-generating. New concepts and new problem are introduced by raising questions about concepts already studied.
Historically this approach to mathematics is certainly false. The significant concepts, operations, theorems, and even methods of proof were suggested by real situations and phenomena. Mathematics grew out of our experiences in the physical world. For example, as we have a1ready noted in another connection, our method of adding fractions was adopted because the sum so obtained represents what results physically when fractiona1 entities are put together. We could instead add the numerators and add the denominators so that 1/2 + 1/2 = 2/4, but this result does not apply when 1/2 of a pie is added to 1/2 of a pie. Likewise, the properties which mathematical operations possess are not dictated by extending the associative, commutative and distributive laws to the new elements. If matrix multiplication, to be useful, must be noncommutative we abandon commutativity, though we could define a commutative multiplication of matrices. Hence, extending the associative, commutative and distributive axioms to new classes of numbers can lead to useless mathematics. Geometry too arose out of the study of rea1 figures existing in physica1 space and the desire to know the properties of these rea1 figures and space itself.
The historical origins of mathematical concepts and procsses need not of course be the pedagogical approach. However, a valid objection to generating new concepts and operations through older ones is the mean-inglessness of what is introduced. For example, to introduce negative numbers some modern texts ask, What number added to 2 gives 0? They then introduce -2 as the requisite number. As some texts put it, -2 is the unique additive inverse to 2. But this introduction of -2 gives no more understanding than the statement, "Antimatter is that substance which added to matter produces a vacuum", gives any understanding of antimatter.
By generating mathematics through mathematical questions and by extending to new domains laws or axioms that hold in previously established ones, mathematics is isolated from all other bodies of knowledge. It exists for its own sake and is presumably self-sufficient. It then appears that by chance the deductive structures so erected fit some physical phenomena and mathematics can be applied to real problems. However, this seemingly fortuitous value is not utilized. Mathematics in the modern mathematics texts is not applied to real problems. Some authors make minor concessions to applications in the seventh and eighth-grade material. Having eased their consciences they ignore applications in the higher grades.
The isolation from the rea1 world is evident from the artificial problems found in the texts. Beyond the purely technical exercises which serve as drill and which certainly have no connection with the real world, one finds exercises whose character is illustrated by the following.
Dividing a certain numbber by two yields the same result as subtracting fifteen from three times the number. Find the number.
Harry earns three times as much per week as Tom does, while Dick earns eighty dollars a week more than Tom. If Dick and Harry have the same salary, how much does each of the three men earn?
Bill is twice as old as Mary. lf he is exactly ten years older than Mary was last year, how old are Bill and Mary?
The Red Cross knitted fifty sweaters in ten days. The Junior Red Cross assisted, contributing two dozen fewer than the senior organization. How many did the Junior Red Cross knit?
How large is an angle whose supplement contains 21 less than four times its complement?
Here is a science problem: According to the Law of Reflection: i = r. Given that i = (2n + 30)░ and that r = (4n - 10)░, find n. Not a word is included about the meaning of the Law of Reflectiou. It could refer to mental reflection.
The artificiality of the problems is obvious. Their inanity and pointlessness should make any sensible student writhe with mental pain. Of course, these artificial problems have been used in the traditional curriculum also.
One would have thought from the pronouncements of several curriculum groups that real applications would have been incorporated and even stressed at least in some of the new programs. For example, the Comnis-sion on Mathematics in its 1959 report, Program for College Preparatory Mathematics, justified the need for a new curriculum by pointing out that there were many new uses of mathematics in fields such as the exploration of space, nuclear science, the social sciences, psychology, business, and industry. Other groups echoed this thought. But no such applications have been included, to say nothing about the older applications to the physica1sciences.
The neglect of applications has been noted and deplored even by some advocates of the new mathematics. Thus Professor Paul Rosenbloom, one of the active workers on the new curriculum, said in an article on applied mathematics (see the reference to Carrier in the bibliography), "In the writing teams for grades 9 to 11, some of us were disappointed that the people we thought have been advocating applications came up with writing stuff about open sentences and the like." But the appli-cations have not been supplied.
One reason is that the professors and teachers who formulated the new curricula do not know science. The professors were pure mathematicians and the courses taken by teachers were offered largely by these professors, so that the teachers too are ignorant of what mathematics can accomplish. Both groups therefore even prefer a treatment which is purely mathematical because it avoids presenting and explaining a few physical concepts and how to formu1ate physical problems mathematically.
The modernists apparently also want to keep their subject pure. They don't wish to sully it; they desire to remove the dross of earth from which mathematics has risen. But as they wash the ore they keep the iron and lose the gold. A perfect command of the English language is useless if a man has nothing to say, and pure inathematics has little to say to young students. As Bertrand Russell put it, "Mathematics may be defined as the subject in which we never know what we are talking about nor whether what we are saying is true." Though Russell had in mind the logical structure of mathematics his statement describes what is being taught. The contents and spirit of the modern mathematics curricula may suit the mathematical scholar but the relation to the real world has been ignored.
Of course mathematics is not an isolated self-sufficient body of knowledge. It exists primarily to help man understand and master the physica1 world and, to some extent, the economic and social worlds. Mathematics serves ends and purposes. If the subject did not have these va1ues it wou1d not get any place at all in the school program. It is because mathematics is extraordinarily helpfu1 that it is in great demand and receives so much emphasis today. These values shou1d be reflected in the curriculum.
During the last few years many of the curriculum leaders acknowledged that they had neg1ected to point out the applications of mathematics. But their approach to remedying this deficiency is ludicrous. They call upon applied mathematicians of some large researeh laboratories or industrial organizations to supply applications. These men abstract. from genuine applications snippets of mathematics that are indeed involved in applications But the snippets reveal nothing of what is accomplished. They are like salt in a cake. The students are asked to eat the salt in the expectation that they will thereby enjoy the cake.
The isolation of mathematics was attacked by Dr. Alvin M. Weinberg in his article "But Is the Teacher Also a Citizen?" Dr. Weinberg, director of the Oak Ridge National Laboratory, charged that professors are so much absorbed in their own disciplines that they are neglecting to teach students useful knowledge, knowledge that can be applied to other fields, as mathematics is applied to physics, and knowledge that would make them more useful members of society. The new mathematics he terms "a puristic monster."
To present mathematics as self-generating is not only a denial of history but conceals its vital connections with other branches of knowledge. From a pedagogica1 standpoint this approach is most unfortunate because it foregoes the opportunity and great need to give motivation and meaning to mathematics. Since the ideas of elementary mathematics did axise from physical and practical problems, these very problems or more modem equivalent ones could be used to motivate the study of mathematics. We have already pointed out that the gravest defect of the traditional curriculum is the lack of motivation. Instead of remedying this most serious defect the modern curriculum has aggravated it. One can-not motivate young people to learn mathematics with more mathematics. Students who are not interested in solving x + 3 = 4 will certainly not be interested in solving x + 4 = 3.
To isolate mathematics is also to rob it of meaning. The student may be persuaded to study the mathematical function s = 16t2. But the function as such has no meaning. Physically it does represent the motion of a ball that is dropped. The variable s represents the distance fallen in t seconds. Given this interpretation the student can visualize s and t increasing as the ball falls, and with a little help he can appreciate how this function differs from s = 16t or s = 16t3. Indeed, the physical appreciation of how the various functions differ is the surest way to convey understanding of the nature and behavior of these functions.
By isolating the subject, mathematics becomes pointless and unattractive. It is as if the subject were taught in a room with mirrors on the walls rather than with windows to the outside world. The modern mathematics leaders have assumed that mathematics taken in and for itself is attractive to young people. But this is hardly true. To the student mathematics proper appears as no more than a huge intricate puzzle. Pure mathematics may provide challenging problems - but so do law, eco-nomics, and biology, and these subjects appear far more vital and relevant to the students. Mathematics, by reasons of its abstractness, is not a natural human interest. The very fact that only a few civilizations among hundreds have devoted some time and effort to the subject may show how unnatural the subject is.
The modern mathematics advocates are of the opinion that students will flnd values in studying mathematics for its own sake. One of the values they extol is structure. Indeed structure has become the fashionable word. Thus the Preface to the course in matrix algebra fashioned by the School Mathematics Study Group states, "The discernment of structure is essential, no less to the appreciation of painting or a symphony than in the behavior of a physical system; no less in economics than in astronomy." Again in its Preface to the Teachers Commentary on its first yeŃr algebra course, this group states, "The principal objective of this First Course in Algebra is to help the student develop an understanding and appreciation of some of the algebraic structure exhibited by the real number system and the use of this structure as a basis for the techniques of algebra."
Just what is structure? Basically any branch of mathematics consists of definitions, axioms and theorems. This is, structure in the large. However, the properties that hold in one branch may not hold in another. Thus mu1tiplication of any two real numbers is commutative but the multiplication of matrices is not. Consequently the logical structure of the real numbers is different from that of matrices.
What can young students be taught about structure? Given the positive whole numbers, and zero - that is, the counting numbers - it is true that the associative and commutative properties hold for addition and multiplication. However, one cannot subtract 5 from 2 and remain in the class of the counting nuinbers. A1ternatively one can say that 3 has no inverse in the class of the positive whole numbers; that is, there is no positive number a such that 3 + a = 0. On the other hand, in the class of the positive and negative whole numbers, 3 does have an inverse, namely, -3. Hence the positive and negative whole numbers possess a property that the positive whole numbers alone do not possess. Thus the two classes of numbers differ in structure.
It is not possible in the class of the positive and negative whole numbers to divide every number
by another. Thus 1/7 does not exist in this class. Alternatively one can say that there is no inverse to multiplication
in the class of the whole numbers; that is, there is no number x such that
7 x x = 1. On the other hand, in the class - of positive
and negative whole numbers and fractions, each number does have an inverse with respect to multplication. Hence
in this class every number has an inverse with respect to both addition and multiplication, so that the structure
of the rational numbers (positive and negative whole numbers and fractions) differs from that of the whole numbers.
Since the high school students do not go much, if at all, beyond the use of real numbers, that is, rational and irrational numbers, they do not have occasion to learn many structures or the opportunity to learn more diverse structures. Nor can they compare many structures as to similarities and differences. Nevertheless, any number of proponents of modern mathematics stress the learning of structure. Beyond the quotations already given we find the Commission on Mathematics stating in its Program for College Preparatory Mathematics (p. 2): "The contemporary point of view, while not discounting the manipu1ative skills necessary for efficient mathematical thought, puts chief emphasis on the structure or pattern of the system and on deductive thinking." Again in the pamphlet The Revolution in School Mathematics, published by the National Council of Teachers of Mathematics, Kenneth E. Brown of the U.S. Department of Health, Education, and Welfare, states, "Another area of emphasis common to alI improved programs is structure. It is reflected in the careful development of mathematics as a deductive system."
There is nothing intrinsically wrong with the goal of teaching structure, though one might question its importance at the elementary stage of mathematical learning. However, the possibility of teaching structure meaningfully is certainly in question. To appreciate the differences and similarities in the structure of the members of our physical world one must meet and know weIl a great variety of animals. One who knows only cats and dogs will readily believe that all animals have the same structure and in fact it will not even occur to him to think about structure. If, however, he meets giraffes, elephants, fish, and birds the subject of structure may strike him as worthy of investigation.
The elementary and high school student is in the position of a man who knows on1y cats and dogs. It is true that one can differentiate between the logical structure of the whole numbers and the signed integers and between the signed integers and the rational numbers. However, the student is still struggling to understand these numbers and the operations with them and is not prepared to take the overall view which the appreciation of structure requires. Even if he glimpses some differences in the operations permissible with rational numbers as opposed to the integers, he is not likely to be impressed with the concept of structure. If he continues with mathematics and encounters algebras wherein mul-tiplication is not commutative, he may then begin to take notice of differences in structure. It is unrealistic to expect people who have seen on1y doghouses and pig-pens to appreciate architecture.
Another of the claims made for the teaching of structure is that it unifies a body of mathematics because it shows that the theorems all follow from one set of axioms and are arranged in a logical sequence. But this facet of structure has very little value to high school students. Elementary algebra in the modern mathematics curriculum remains the usual hodgepodge of disconnected topics that it is in the traditional curricu1um. The fact that all of these topics can be treated from one basic set of axioms may give them unity in the mind of a mathematician but this is hardly a unifying or impressive connection especially to young people who have yet to learn what a deductive structure is.
Mathematics teachers do often talk about giving the students a feeling for the power of mathematics, and they also speak of doing it through exhibiting the structure and order which permeate every branch of the subject. Just how these features make evident the power of mathematics is not clear. To demonstrate this power one must use it in real situations. This is where the power is applied and this is how students will get to appreciate it.
Thus the core of the criticism of teaching structure to young people, aside from its importance or lack of importance, is that the subject cannot be significant at this stage. And this very fact implies that it should not be taught at this level.
CHAPTER 8 - The New Contents of the New Mathematics
"Wisdom oft is nearer when we stoop than when we soar."
William Wordsworth
Logical development as the road to understanding, rigor, precision through terminology and symbolism, and emphasis on mathematics for its own sake are all employed in the modern mathematics approach to the curriculum. What subject matter is favored? The old subjects, arith-metic, algebra, Euclidean geometry, trigonometry, and the elements of analytic geometry are still taught in the new curriculum, despite the claim made by many modernists that this pre-1700 mathematics is outmoded and even useless in modern society. Of course, the amount of traditional material taught varies somewhat from one version to another of the modern mathematics curriculum but it is the predominant part in every case.
However, the new curriculum does offer some new contents. By far the most emphasized among the new topics is set theory. This subject is now taught from the kindergarten up, as though students would starve, mentally at least, if they did not have this diet. A set, as any modern mathematics text will tell us, is no more than a class or collection of objects. A set of apples, a set of garbage cans, a set f letters §f the English a1phabet, and the set of natura1 numbers are examples. The concept and the word set are simple enough. However, set theory contains many subtle concepts and theorems. The two basic concepts are the union of two sets and the intersection of two sets. By the union of the set of red objects and the set of books we mean the set of all objects that are either red or are books. The intersection of these two sets is the set of all objects common to the two. Thus, since a book with red covers is a red object, then the set of red books is the intersection of the two sets. One can now speak of the union and intersection of three or more sets and combinations of unions and intersections. A set usually has subsets. Red chairs would be a subset of all red §bjects. One subset is contained in every set and this is the empty set. This set could stand for the set of women presidents of the United States.
The most significant sets are infinite sets. Thus the set of natural numbers is infinite. Students are taught that two sets are eqniva1ent if it is possible to set up a one-to-one correspondence between them. By means of the correspondence there is a one-to-one correspondence between the set of natura1 numbers and the set of even natural numbers, in that each natural number corresonds to double itself and conversely. These two sets and indeed any set that can be put into one-to-one correspondence with the natural numbers are said to have the same number of objects. So there are as many even numbers as natural mumbers despite the fact that the even numbers are only a part of the set of natural numbers. Students are then shown that the set of rational numbers and the set of natural numbers can be put into one-to-one correspondence so that there are as many rationa1 numbers as natural numbers. They are also taught that the set of real numbers cannot be put into one-to-one correspondence wýth the natura1 numbers, and since the set of real numbers contains the natura1 numbers it is a larger set than the set of natura1 numbers.
The emphasis on sets is justified by the modem mathematics proponents on several grounds. The first is that it is a basic concept of mathematics. Thus, numbers are names for sets of objects (though the union and inter-section of sets are not the same operations as addition and multiplication of whole numbers). The second contention is that the concept of set unifies various branches of mathematics. Thus the notion of set is used to speak of a solution set for the roots of equations, to define geometrical figures, and to define relation and function in terms of sets of ordered pairs of numbers. The unification through sets, at least on the elementary level, is limited to special terminology and a questionable refashioning of previously accepted and acceptable definitions of concepts.
Perhaps the second most popular topic of modern mathematics is bases of number systems. This concept dates back to the Babylonians of 2500 B.C. who used base sixty. The concept was thoroughly aired by the fa-mous mathematicians John Wallis and Gottfried Wilhelm Leibniz in the seventeenth century.
Just what is a base? Our method of writing quantities presupposes base ten. Thus 372 means 3 x 102 + 7 x 10 + 2. The same quantity can be written in another base, say eight. Since 372 = 5 x 82 + 6 x 8 + 4, written in base eight is 564. Students are taught ta write nurnbers in other bases and how to add and multiply in these bases. It so happens that modern electronic computers operate in base two. One might expect, then, that students would be taught bases when they are about to learn about computers. But the contention of the modern mathematics proponents is that learning how to operate in bases other than ten aids the understandÝng of base ten and the operations of arithmetic.
A third common topic in the new mathematics is the study of congruences. This subject is frequently
introduced by what is called clock arithmetic. Our clocks record up to twelve, and then start over again with zero.
Thus if twenty-two hours have passed from twelve o'clock, the clock will not read 22 but 10. This suggests that
all numbers be reduced by as many twelves as can be subtracted from them. Twenty-two will be reduced to ten and
is said to be congruent to ten modulo twelve. To make the arithmetic simpler students are taught congruences modulo
five or modulo six. Now, congruences have no application to science or engineering. They are taught for their mathematical
interest and, as a matter of fact, the topic belongs to the theory of numbers, which
is a subject pursued primarily for its own sake. Nevertheless it is a curiosity and may awaken some interest in
numbers. One does have to make up new addition and multiplication tables. Thus modulo 6,
4 x 3 = 0 because if one takes the normal product of twelve and sub-tracts as many sixes as possible, one obtains
zero. This product also illustrates another curious feature, namely, that the product of two numbers can be zero,
though neither factor is zero.
Another topic favored by the modern mathematics curriculum is inequalities. A simple example would call for the values of x for which 3x < 6. This topic has been taught in the traditional college algebra for many generations, but the new curriculum has moved it down to ninth-grade algebra.
The subject recommended for the second semester of the twelfth grade by the School Mathematics Study Group is matrices. A matrix is a rectangular, usually square, array of numbers. Thus
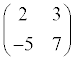
is a matrix and is said to be of second order because it has two rows and two columns. Such matrices can be added, subtracted, multiplied and usually divided by one another. They can also be converted into matrices with different numbers by multiplying them by other matrices. In other words, there is an algebra of matrices.
Many modem curricula teach symbolic logic. In ordinary reasoning we combine statements in various ways. Thus one might say, "It is not raining" and "I am going for a walk". Here the two statements, "It is not raining" and "I am going for a walk" are independent propositions connected by the conjunction "and". The joint assertion of these two propositions p and q is evidently true if and only if both propositions are true. However, this evident meaning is not accepted as such but is defined what is called a truth table which looks as follows:
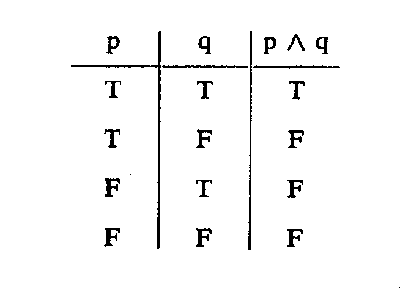
The symbol ^ means "and"; the truth table tells us that the joint assertion is true if and only if p and q are both true. Presumably the truth table is more informative and more precise as a definition of "and" than the verbal statement. There are similar truth tables for "or", "implication", and "negation". These truth tables are then used to prove theorems of logic. Thus one proves by this means that the negation of the assertion "it is not raining and I am going for a walk" means either that it is raining or I am not going for a walk or both. One is supposed to learn how to reason through the use of these, truth tables.
Many moder˝ texts teach Boolean algebra which is a1so intended to aid in reasoning and is an a1temative to the use of truth tables. The algebra is the same as the a1gebra of sets. For example, the set of dogs plus the set of dogs is just the set of dogs in set theory. In Boolean algebra if a represents the set of dogs, the algebraic statement is a + a = a. If b represents the set of animals, the statement that all dogs are animals is represented by ab = a, wherein ab means the set of objects in a and in b. By using Boolean algebra one can perform ordinary reasoning in purely symbolic form.
Modern mathematics texts favor abstract concepts. Before students. have worked with functions
they are asked to learn about relations and functions in terms of sets of ordered pairs (Chapter 6). It is only
after the general definitions are taught that students leam to work with y = x2,
y = x3, and the like.
To get the students to practice abstraction they are asked to answer exercises such as the following:

This exercise reŃlly asks, "For which of the ![]() defined on the right side of each equals sign can x and y be interchanged
without altering the express´on?" (The answer is d.)
defined on the right side of each equals sign can x and y be interchanged
without altering the express´on?" (The answer is d.)
In keeping with the emphasis on abstractions and structure the modern mathematics texts introduce the notions of group and field. A group is any collection of elements and an operation which satisfy severa1 condi-tions. If we call the operation addition (though it may not be at all the addition of rea1 numbers) then one condition is that the sum of any two elements must be another element of the collection. The associative property must apply to the operation of addition. There must be an element denoted by 0 such that a + 0 = a for every element a of the collection. Finally, to each a of the collection there must be another element, denoted by -a, such that the sum of a and -a is 0.
The simplest example of a group is the set of positive and negative whole numbers and the operation of addition. However, the importance of the group notion lies in the fact that there are many different collections of elements and an operation associated with each collec-tion which form a group.
The concept of a field applies to a collection of elements and two operations, called addition and multiplication; each of these operations must possess the properties that the group operation possesses (with an exception with respect to 0) and the two operations are related by the distributive law, that is, a x (b + c) = a x b + a x c.
The simplest example of a field is the collection of rational numbers (whole numbers and fractions) with the usual operations of addition and multiplication. As in the case of groups there are many collections of elements and operations that form a field.
The students are expected to learn not only the concepts of group and field but properties of these structures beyond the ones involved in the definitions. The study of these abstract structures and their properties is usua1ly taught in the third or fourth year of the traditional undergraduate curricuium and only to majors in mathematics. In the new mathematics some of the concepts are taught in elementary school and the subject proper is taught in the fourth high school year.
Students are asked to learn abstract concepts in the expectation that if they learn these, the concrete realizations will be automatically understood. Thus if a student learns the genera1 definition of a function, he will presumably understand the specific functions he will have to dea1 with; and if he learns what a field is, he will know all about the rational numbers, and other mathematica1 collections that form fields. Phrased in terms of abstract versus concrete, one can say that modem mathematics favors the abstract as the approach to the concrete.
That abstract subject matter was to be featured was indicated early in the movement. For example, in its 1959 report the Commission on Mathematics of the College Entrance Examination Board states (p. 20), "The goal of instruction in a1gebra should not be thought of exclusively or even largely as the development of manipulative skills. Rather instruction should be o˝ented toward the development and understanding of the properties of a number field." For the second semester of the twelfth year the Commission recommended a choice between introductory probability with statistical applications and an introduction to abstract algebra stressing groups and fields.
We have described the new contents of the modern mathematics cur˝culum. Presumably it meets the needs of young students entering int~modern society. Apparently it should also appeal to them because, as the authors of The Revolution in School Mathematics put it (p. 32) "He [the studentl wants to know how mathematics fits into his world. And, happily, his world is full of fancy and abstractions. Thus students become interested in mathematics because it gives them quick access to a kind of intellectual adventure that is enticing and satisfying." Apparently human imagination is not dead.
Let us review the content of the new mathematics in the light of the claims made for the new curriculum.
The modem mathematics proponents have made much of the point that the mathematics taught in the traditional cur˝culum was all known before 1700 and that students were bored witb such outdated mathematics. Moreover, the proponents claimed, the modern age requires totally new mathematics. How modern are the contents of modern mathematics?
Actually, most of the materal in the modern mathematics curriculum is the traditional material. The old arithmetic, algebra, geometry, trigonometry, analytical geometry, and calculus are all there and are in fact the core of the new curriculum. Hence the word modern is certainly inapprop˝ate. The charge that the traditional curriculum is outmoded is belied by the very admission of the modernists that they offer primarily a new approach to the old curriculum. Despite this fact the proponents began and continue their campaign on the major platform that the present age requires new mathematics for such applications as linear programming, operations research, game theory, quality control, and other fields. Actually these applications use traditional mathematics.
Even if the new cur˝culum had abandoned the older contents on the ground that it was all created by 1700 would the new curriculum be any better? Would the traditional curriculum then be three hundred years behind the times? Such an argument might apply to history but it has no force when applied to mathematics. Our subject is cumulative. The new builds on the old, and the old subject matter must be understood if the new developments are to be mastered. Hence a curriculum based solely on post 1700 mathematics would have no foundation.
One cannot defend all that is old. We have already noted (in Chapter 2) that the logarithmic solution of triangles, a favorite topic in the traditional trigonometry, has lost its importance. It can be discarded. But there is very little in the traditional curriculum that can be declared outmoded or useless today. Mathematics has been compared to a great tree ever putting forth new branches and new leaves but nevertheless having the same firm trunk of established knowledge. The trunk is essential to the support of the life of the entire tree.
However, the new curriculum does include some new content. In evaluating these new topics let us keep in mind that elementary and high school students do not know what they plan to do later in life. Even the few that think they do may change their minds several times. So whatever mathematics courses offer should be valuable in the full variety of careers that these students may take up.
The new topic that receives the most emphasis in modern mathematics is set theory. Now there is no question that the word "set" is useful. It means no more than collection, class, group, and the like, in the usual nontechnical sense. However, as we have already noted, students are asked to learn union and intersection of sets, subsets, the empty set, infinite sets, one-to-one correspondence between inflnite sets, larger and smaller infinite sets and other concepts. All of this is a sheer waste of time. In very sophisticated and advanced theories of mathematics set theory plays a role, but in elementary mathematics it plays none. In fact it is almost certain that set theory was brought in to give the new mathematics the air of being sophisticated and advanced rather than because it is helpful; It happens to be one of the few topics of advanced mathematics that can be presented without requiring probibitive background, and it is no doubt one of the few topics of advanced mathematics that some of the framers of the modern mathematics curricula could grasp.
Having introduced set theory the curiculum makers must use it. They invented a teminology and definitions which do so. Thus to speak of the "solution set of x + 2 = 4", instead of the va1ue of x for which x + 2 = 4, uses set language. To speak of a triangle as the "union of three noncollinear points and the line segments joining them", replaces the expression three noncollinear points and the line segments joining them. The point of intersection of two lines is described as the set intersection of the two linear sets. Functions, as we noted earlier,are sets of ordered pairs. This definition of function is particularly unfortunate. What is important about a function, say, y = x2, is that as x varies so does y and the values of y depend upon the values of x. All of this meaning is vitiated in the definition as a set of ordered pairs. In fact the set of pairs is infinite and cannot be ordered by the mind so as to see the important concept of variation. These uses of set theory, then, distort the basic concepts.
Professor Feynman, whom we have already cited as having examined textbooks for use in the state of California, says, "In almost all of the textbooks which discuss sets, the material about sets is never used - nor is any explanation given as to why the concept is of any perticular interest or utility. The only thing that is said is - 'the concept of sets is very familiar'. This is, in fact, true. The idea of sets is so familiar that I do not understand the need for the patient discussion of the subject over and over by several of the textbooks if they have no use for sets at the end at all."
The role of set theory in mathematics may be worth noting because it gives some indicatýon of how the modern mathematics curriculum has approached mathematics. This role may be understood through an analogy Suppose that, because of genera1 dissatisfaction with our country's production of musicians, we decided to change music education. Some group of educators might come along and argue that we have failed to make progress in music because we are still teaching Bach, Beethoven, and Brahms. We must instead teach modern music. More than that, we must teach the physical foundation of music. Now the physical foundation of music is basically the physics of sounds, musica1 sounds in particular. Hence music students would be taught primarily the theory of sound to the detriment of playing music, listening to music, and appreciation of the great works of the past. One could of course maintain that the physics of musica1 sounds is a desirable subject in itself. This is true. But expertise in that subject, assuming even that it is pedagogically accessible to young people, will not produce musicians.
The same argument can be made with respect to the teaching of painting. One could teach the theory of colors and develop experts in this area. But these experts might not be able to paint a stroke -at least on the basis of their education in colors.
Similarly, set theory - though logically the foundation of a sophisticated and rigorous approach to mathematics - is of no use at all in understanding and learning to work with elementary mathematics.
As a matter of fact, set theory can be confusing even in the context where it is claimed to be most helpful, namely, in learning about numbers. The best the modern texts can say about the relation of number to set is that number is a property or a name of a set. This in itself is so vague as to be useless as a definition of a whole number. But the situation is worse than that. Given the two sets{1,2,3) and {3,4,5}, the union of the two sets is the set{1,2,3,4,5), which contains only five objects. But adding the number of objects in the first set to the numher of objects in the second gives 6. Likewise, the interection of the two original sets is the set {3}. But the product of the two numbers represented by the two sets is 9. Hence union and intersection, the two basic operations with sets, do not correspond to adding and multiplying the numbers represented by the sets.
A critical examination of the uses of set theory in. elementary and high school texts refutes the claim of the modernists that set theory unifies mathematics. Beyond using it artificially to define concepts, no signifi-cant use is made of the subject. The whole subject is in fact dropped and only the vocabulary survives in the later development. There are, of course, deep results within the area of set theory, but even the modernists recognize that these lie far beyond the province of elementary mathematics. In this matter we may compare set theory with elementary geometry. When first encountered, the axioms of geometry must seem immediately obvious to the student, and to this extent geometry and set theory start out on a par. But almost before he realizes that anything of moment is being developed in geometry, the student comes upon consequences that surprise and may excite him. From seemingly simple axioms and the deductive mode of reasoning emerge such unexpected and heady results as that the medians of a triangle meet in a point, as do the altitudes, the angle bisectors, and the perpendicular bisectors of the sides - and not just for one type of triangle but for every triangle. To a mathematically sensitive student, such results come as a never-to-be-forgotten revelation of the power of abstract mathematical reasoning. There is nothing comparable in the rudimentary treatment of set theory in the new mathematics curriculum.
Set theory is for elementary mathematics a hollow formalism which encumbers ideas that are far more easily understood intuitively. The attempt to involve it is almost ludicrous and a travesty of pedagogy. The theory of sets has not proved to be the elixir for mathematical pedagogy.
The emphasis on set theory has led to caustic criticisms; Not atypical is the following: "One writer urges that the students become active participants in an adventure in the learning of concepts. And what is this adventure? The students give the teacher their own examples of sets. They begin with sets of rather similar things; but soon the adventure has risen to the pitch where they can contemplate such sets as 'the nose of the notary, the moon, and the number 4'. The students have been led with great pedagogical skill to the breathtaking conclusion that any collection of things is a collection".
Another critic was equally severe. "Oh see, Johnny has a set of marbles. Look, look, Billy has a set of marbles. See Billy's set. Here comes Mary. Mary gets all the marbles. Mary gets the union of Johnny's set and Billy's set. See Marys union".
The second new topic espoused by the new mathematics is bases of number systems. As we have already pointed out, this topic is not new historically nor is it new in the teaching of mathematics. It has been taught for generatýons in college algebra. Hence what is new is merely that the topic has been introduced at the elementary school level. The contention is that students will understand the usual base ten method of writing numbers better if they learn how to write them in any base.
Pedagogical problems are dificult to resolve. Perhaps a fair analogy to teaching bases early would be to teach students French while they are still learning the rudiments of English. Would they learn English better? It is more likely that learning two languages - simultaneously would be confusing. One might improve and deepen his knowledge of English by learning French but this would best be done after the command of Eng-lish is reasonably well established. Another analogy might be learning to play the piano and violin at the saine time.
Another often encountered argument for the introduction of bases is that modern electronic computers use base two. Computers do use base two, but it would seem more pertinent to teach base two when students are about to learn how to use computers rather than in the arithmetic of the second, third, or fourth grade.
Congruence is a third new topic. This, we may recall, involves arithmetic modu1o twelve, or five, or six. There is no application of this concept on an elementary Ievel. It may intrigue students but at the expense of learning something more important and perhaps equally intriguing. There seems to be nothing to recommend this topic for the elementary level except its novelty.
As to inequalities - another of the topics now featured in modern mathematics texts - this, like bases, was commonly taught at the college algebra level and all that has been done is to bring this topic down to the high school level. Very little can be done with this topic at the high school stage. Even when taught at the college level it was not used for some time thereafter. Hence there is even less point to teaching it at the lower level.
Boolean algebra, another of the new topics, is very much like set theory so far as union and intersection are concerned. Primarily it is a step in the direction of mathematical logic. Teaching it at the high school level is now defended on the ground that it is used in the design of switching circuits, especially in computers. The defense seems weak in view of the fact that elementary and high school students do not know what careers they will follow, so that elementary and high school education should be broad rather than pre-professional. How many high school students will design switching circuits later in life?
Still another topic of the modern curriculum is symbolic logic. There are many reasons for not teaching it to young people. There seems to be a prevalent but nonetheless mistaken belief that symbols explain concepts or ideas. Presumably the meaning of a joint assertion of two propositions such as "It is raining and I am going for a walk" is explained and even defined by a truth table. This is putting the cart before the horse. How was the truth table obtained? Evidently we have to know in advance that the joint assertion of two propositions is true if and only if both are true. Then we can construct the truth table. The attempt to reason through the meanings supplied by truth tables is inefficient, clumsy and even baffling. No mathematician or lawyer reasons in this way. And no mathematician except a specialist in symbolic logic uses symbolic logic. Rather, every mathematician thinks intuitively and then presents his arguments in a deductive form using words, familiar mathematical symbols and common logic. Specialists in foundation problems, who have to worry about the ambiguities and imprecision of ordinary lan-guage, do resort to symbolic logic. But even these people know intuitively what they want to say and then express their thoughts in special symbols. The symbolic logic does not control or direct the thinking; it is merely the compact written expression of the real thinking. Indeed, one must make sure that the symbols express what is intended rather than that the symbols tell him what he means to say. Not only is symbolic logic not used by, most mathematicians but those who do use it do their effective thinking in common language.
One of the subjects recommended for the twelfth-grade course and rather widely adopted is an introduction to abstract algebra. In many texts this course stresses matrices, the nature of which we described earlier. There is an extensive algebra of matrices and students are taught how to add, subtract, multiply and divide matrices as well as many other operations. However, matrices are themselves abbreviated forms of what are called transformations and the students at the twelfth-grade level have no background in the significance and uses of transformations. Hence they learn merely to manipulate mat˝ces to no purpose, and they cannot have any feeling for or make sense of what is accomplished because they do not know the context in which matrices are useful. This manipulation of matrices becomes, then, a series of mechanical tasks - as mechanical as the traditional teaching of algebra, which has been justly criticized. The a1gebra of ordinary numbers is at least a necessary step to progress in elementary mathematics; and while no case can be made for meaningless mathematics of any sort, there is some reason to teach the a1gebra of ordinary numbers to high school students. There is no justification for teaching matrices at the twelfth-grade level.
Another component of the recommended abstract algebra course is the study of groups and fields. We have already explained that these are abstract formulations. of various, more concrete algebras. The abstract versions are studies of structures common to the concrete cases. The argument against teaching such structures is simply that it is premature. One might as well try to teach the structure of all languages -they do have common features - to a child who has yet to leam the English language. Once a student has learned the algebras of real numbers, complex numbers, rational functions, matrices, vectors, transformations, and congruences, it may enlighten him to know that these algebras do or do not have some common features. One can then even prove a theorem about groups and the theorem will apply to all those concrete algebras which form groups. There is, in other words, an advantage to proving the abstract theorem once and for all so as to cover many special cases in one swoop. However, the abstractions themselves are meaningless if not preceded by effective learning of specific algebras, and the advantage of proving a general theorem in the abstract aIgebra will hardly be impressive to one who knows on1y one instance of a group or a field - and knows it imperfectly at that.
The very point of an abstract formulation is that it unifies and reveals common properties in concrete and familiar branches of mathematics. Therefore, abstraction is not tbe first stage but the last stage in a mathematica1 development. It may give insight, but only into concrete structures already well learned. It unifies, but only what one already knows. Without much previous knowledge of concrete cases the abstract concepts remain empty, arbitrary children of mathematical fantasy. To confront youngsters with abstractions that lie above their level of maturity is to create bewilderment and revulsion rather than increased knowledge. In brief, the highly abstract concepts cannot be exploited at an elementary level.
There is another objection to teaching the abstract structure prematurely. It is true that the rationa1 numbers, the real numbers, and the complex numbers each have the properties of a field. That is, the sum, product, difference and quotient of any two rationaI numbers is a rationa1 number and the same is true for real numbers and for complex numbers. One could therefore argue that the students do have three concrete examples of a field. Should the field concept then be taught early? The answer is still no, because the field properties are those which are common to all these systems of numbers, so they automatically wipe out any distinguishing features. But the operations with rational numbers are different from those for real numbers and the latter are different from those for complex numbers. Thus the product of the fractions 3/4 and 7/8 is 21/32; the product of \/2 and \/3 is \/6; and the product of 2 + 3i and 4 + 5i is -7 + 22i. Until the student can at least operate freely with rational and real numbers, there is little point in his knowing that a x b = b x a is a property of fields. A student who knew perfectly the properties of a field cou1d not necessarily make change in a grocery store, much less balance a check book. Let us keep in nund that the more genera1 the mathematica1 concept, the emptier it is.
To put it another way, fields do not explain the types of numbers and operations with them. In fact it is just the reverse. A good understanding of the several number systems explains the concept of a field. Hence, the familiar argument that it is efficient to teach the abstract concept early because it comprises several concrete cases at once is groundless. So far as efficiency is concerned, the time that is wasted is the time spent teaching the abstract concept. When one takes into account that perhaps fifty per cent of the students entering college cannot add and mu1tiply fractions, especially if letters are involved, one can see where the emphasis must be put.
Psychologically the teaching of abstractions first is all wrong. Indeed, a thorough understanding of the concrete must precede the abstract. Abstract concepts are meaningless unless one has many and diverse concrete interpretations well in mind. Premature abstractions fall on deaf ears.
In a real sense one cannot teach an abstraction. The difficulty posed to the student is analogous to giving him a correct biological definition of dogs and then showing him a poodle and a collie as examples. When presented with a bull terrier and asked if that is a dog, the student may still be baffled. The biological definition contains so many broad and technical terms that he may not really understand it; if so he cannot apply it.
Abstractions must grow on people. They cannot be handed down ex cathedra. As people's expe˝ences with the different varieties of functional relationships and their peculiarities increase, they will gradually see the wealth of situations wbich have a basic idea in common; at this stage they will be enlightened if this common idea is pointed out. They will a1so appreciate the various conditions or qualiflcations that must be incorporated in a general deflnition.
To start with a general concept and then to use it only in special cases, which is the practice in modern mathematics, is pedagogically absurd for another reason. One may wish to teach a six-year-old a little about dogs so that he may play with them and at the same time be cautious around them. Would one start with the biologicaI definition? Leaving aside whether the definition is meaningful to the youngster, we shou1d ask whether it is helpful to know it. Would it not be far more practical for this youngster to learn about the particular dogs that he will meet in his environment? So it is with the mathematicaI concepts. The general definition of a function is useless as long as the immediate objective is to learn about y = 3x, y = 3x + 7, y = x2 and the like. In fact, the genera1 definition burdens the student with a mystery which clouds all his subsequent thinking. A year or two after learning a definition of function applicable only to simple cases, he may need a slightly broader notion of function - for example, when he meets functions of two or three variables. Even then the general definition is useless. It is sufficient to extend the term function to include, for example, z = x2 + y2.
The human mind operates no differently in mathematics than in political or social thought. One may preach the brotherhood of man, but this preaching does not get people to understand and practice brotherhood. Teaching young children to get along with and respect others of different races and creeds in daily acts may achieve brotherhood, but the general ethical principle wiIl make no impression. Students who are taught abstractions before they have acquired the rich experience which in fact led to those abstractions may acquire superficial knowledge and be able to mouth words. But they cannot be said to really understand these abstractions.
The modern mathematician's preference for abstractions is reminiscent of a story. The principal of a school boasted of how much he liked his students and about how much he was concerned for their welfare. One day he saw a student walking on a freshly laid concrete side-walk. He rushed over and roughly yanked the student off the fresh concrete. A teacher who saw the incident reminded the principal of his professed concern for students and chided him for his rough handling of the boy. The principal replied, "I like students in the abstract but not in the concrete".
The new mathematics advocates, countering the charge of too much abstraction, have cited tbe Harvard psychologist Jerome S. Bruner who said, "Any subject can be taught in- some intellectublly honest form to any child at any stage of development." The saving feature of this doctrine is its vagueness. Leaving aside the question of whether the particular abstractions that any - one group may be interested in promoting warrant priority, one wonders how one could present the substance of Kant's Critique of Pure Reason even to high school students. What can happen and does happen when Bruner's Doctrine is taken too seriously is that students accept the abstractions docilely and are as understanding and as critical of what they are taught as children are when they learn a catechism.
The tota1 picture presented by the new topics in the modern curriculum is hardly impressive. Some items, such as bases and inequalities, were merely pushed down from the levels at which they were previously taught, with no gain and much reason to question. Others, such as congruences, are at the elementary level pointless novelties. Still others, such as Boolean algebra and symbolic logic, are specialities that should be reserved for specialists. And finally, the advanced topics, set the dry, matrices, and abstract a1gebra, seem to have been deliberately chosen to show that the curriculum has caught up with advances in mathematics even though these advances have no proper place or function in the training of youngsters. So far as the advanced topics are concerned, the "reformers" seem to be under the impression that what smacks of modern mathematics is modern mathematics - rather like the small boy who thinks that because he wears long pants he is a grown-up.
Though severaI capable and broadly educated mathematicians participated in framing the nuinerous versions of the new mathematics, their contributions were highly diluted. The new mathematics as a whole is a presentation from the point of view of the shallow mathematician, who can appreciate only the petty deductive details and minor pedantic, sterile distinctions such as between number and numeral and who seeks to enhance trivia with imposing-sounding terminology and symbolism. This mathematics offers an abstract, rigorous version that conceals the rich and fruitful essence and emphasizes uninspiring generalities isolated from all other bodies of knowledge. It stresses final sophisticated versions of simple ideas while treating superficially the deeper ones - and so necessarily assumes a dogmatic character. The formalism of this curriculum can lead only to an erosion of the vitality of mathematics and to authoritarianism in teaching, the rote learning of new routines far more useless than the traditiona1 routines. In brief, it presents form at the expense of substance and substance without pedagogy.
Perhaps the decisive criticism of the modern mathematics program was made unwittingly by a professor who was evidently pleased with it and who intended his remark to be words of praise: "If they [the students] are going to fail mathematics, they might just as well fail good mathematics".
When one criticizes the modern mathematics program one often finds that the listener, wishing to be sympathetic and not knowing where to stand, remarks that undoubtedly the truth lies between the traditional and the modern mathematics versions. Such a compromise may be correct in some controversies, but it is not applicable here. If someone argues that the earth turns from east to west and another that the earth turns from west to east, one cannot compromise, however well-meaning one may be, by saying that the truth lies between these alternatives. As we shall see later in Chapter 11, the proper reform is diametrically opposite to the path taken by modern mathematics and lies, so to speak, on the other "side" of traditional mathematics.
Copyright ę Helen M. Kline & Mark Alder 2000
Version 30th March 2018
|