Why Johnny Can't Add: Up to Chapter 2

For many generations the United States maintained a rather fixed mathematics curriculum at the elementary and high school levels. This curriculum, which we shall refer to as the traditional one, is still taught in fifty to sixty per cent of the American schools. During the past fifteen years a new curriculum for the elementary and high schpols has been fashioned and has gained rather wide acceptance. It is called the modern mathematics or new mathematics curriculuin. Though many groups have contributed to it and their recommendations are not quite identical, for present purposes I believe that it is proper and fair to overlook the differences among them.

The experimental work on the new curriculum, such as it was, has been done. Hundreds of new texts have been written and millions of children and young people have been and are being taught with this new inaterial. In addition, several dozen books have been published which explain the new curriculum to parents, teachers, principals, superintendents, and other interested parties. The money, time, energy, and thought expended on this program have been considerable -even enormous.

Mathematics occupies a centra1 position in the schools. Students spend eight years on it in the elementary schools and from two to four years in the high schools. - Moreover, the subject has proved to be an obstacle to scholastic achievernent for many students. Hence the question of whether the new curriculum has actually improved the teaching of rnathernatics and has indeed made the subject more accessible to the students is important.

Now that the new program has been somewhat stabilized and its nature made clear, it seems possible and necessary to decide whether progress has actually been made. Are our chíldren really better off by reason of this nationwide, highly touted reform? Certainly the education of our children is too important for us to accept a curriculum uncritically just because it has been extensively proinoted and has been backed by many professors of mathematics.

Up to the present time it has been assumed by the genera1 public that the profession has spoken and that the ouly problem is how to extend the teaching of the new curriculuin to more and more schools. However, sharp difierences of opinion as to the merits of the innovations do exist among professional mathematicians and teachers. It behooves all interested parties to examìne the effectiveness of the new material lest the innovations become established as the new orthodoxy despite the absence of any firm evidence that the innovations are genuine improvements. This is what I propose to do.

I hope that the reader wifl feel, as I do, that any book critical of a particular attempt at reform is not ipso facto reactionary. The traditional curriculum has major defects and I shall cite them. It needs to be improved. But it seeins to me that true progress is possible - and a truly progressive attitude can exist - only if we have the courage to admit that any particular attempt at reform has not worked.

I am indebted to many people for helpful criticisms and suggestions but especially to Professor Fred V. Pohle of Adelphi University, Professor Alexander Calandra of Washington University, and to Dr. George Grossman, Director of Mathematics for the New York City Board of Education. I am a1so indebted to Mr. Thomas McCormack, president of St. Martin's Press, not only for criticisms and suggestions, but for his encouragement to publish this book. He stressed repeatedly that a critique of the mathematics curriculurn would be a public service. Of course the particular views expressed herein are chargeable only to myself.

Morris Kline

1973

CHAPTER 1 - A Taste of Modern Mathematics.

".. . Great God! I'd rather be
A Pagan suckled in a creed outworn;
So might l, . .
Have glimpses that would make me less forlorn."

William Wordsworth

Let us look into a modern mathematics classroom. The teacher asks, "Why is 2 + 3 = 3 + 2?"

No, reproves the teacher, the correct answer is because the commutative law of addition holds. Her next question is, Why is 9 + 2 = 11?

"Wrong," the teacher exclaims. "The correct answer is that by the definition of 2,

Now 9 + 1 is 10 by the definition of 10 and 10 + 1 is 11 by the definition of 11."

Evidently the class is not doing too well and so the teacher tries a simpler question. "Is 7 a number?" Thà students, taken aback by the simplicity of the question, hardly deem it necessary to answer; but the sheer habit of obedìence causes them to reply affirmatively. The teacher is aghast. "If I asked you who you are, what would you say?"

The students are now wary of replying, but one more courageous youngster does do so: "I am Robert Sinith."

The teacher looks incredulous and says chidingly, "You mean that you are the name Robert Smith? Of course not. You are a person and your name is Robert Smith. Now let us get back to my original question: Is 7 a number? 0f course notl It is the name of a number. 5 + 2, 6 + 1, and 8 - 1 are names for the same number. The symbol 7 is a numeral for the number.

The teacher sees that the students do not appreciate the distinction and so she tries another tack. "Is the number 3 half of the number 8?" she asks. Then she answers her own question: "Of course not! But the numeral 3 is half of the numeral 8, the right half."

The students are now bursting to ask, "What then is a number?" However, they are so discouraged by the wrong answers they have given that they no longer have the heart to voice the question. This is extremely fortunate for the teacher, because to explain what a number really is would be beyond her capacity and certainly beyond the capacity of the students to understand it. And so thereafter the students are careful to say that 7 is a numeral, not a number. Just what a number is they never find out.

The teacher is not fazed by the pupils poor answers. She asks, "How can we express properly the whole numbers between 6 and 9?"

"No", the teacher replies. "It is the set of numbers which is the intersection of the set of whole numbers larger than 6 and the set of whole numbers less than 9."

A teacher thoroughly convinced of the vaunted value of precise language, and wishing to ask her students whether a number of lollipops equals a number of girls, phrases the question thus: "Find out if the set of lollipops is in one-to-one correspondence with the set of girls." Needless to say, she gets no answer from the students.

Bent but not broken, the teacher asks one more question: "How much is 2 divided by 4?"

"Well," says the student, "you have taught us that division is repeated subtraction. I subtracted 4 from 2 and got minus 2."

It wouId seem that the poor children would deserve some relaxation after school, but parents anxious to know what progress their children are making a1so query them. One parent asked his eight-year-old child, "How inuch is 5 + 3?" The answer he received was that 5 + 3 = 3 + 5 by the commutative law. Flabbergasted, he re-phrased the question: "But how many apples are 5 apples and 3 apples?"

The child didn't quite understand that "and" means plus and so he asked, "Do you mean 5 apples plus 3 apples?"

"Oh," said the child, "it doesn't matter whether you are talking about apples, pears or books;
5 + 3 = 3 + 5 in every case."

Another father, concerned about how his young son was getting a1ong in arithmetic, asked him how he was faring.

"Not so well," the boy replied. "The teacher keeps talking about associative, commutative and distributive laws. I just add and get the right answer, but she doesnt like that.

These minor examples may illustrate, and perhaps caricature, some features of the currìculum now called modern mathematics or the new mathematics. We shall examine the major features in greater detail in due course and we sha1l consider their merits and demerits. But first, we shall revíew briefly the old mathematics to see what defects prompted the development of a new curriculum.

CHAPTER 2 - The Traditional Curiculum

"I have found you an argument but I am not obliged to find you an understanding."

Though the traditional curriculum has been affected somewhat in recent years by the spirit of reform, its basic features are readily described. The first six grades of the elementary school are devoted to arithmetic. In the seventh and eighth grades the students take up a bit of algebra and simple facts of geometry such as formulas for area and volume of common figures. The first year of high school is concerned with elementary algebra, the second with deductive geometry, and the third with more a1gebra (generally called intermediate a1gebra) and with trigonometry. The fourth high schooi year usually covers solid geometry and advanced algebra; however, there has not been as much uniformity about fourth-year work as there has been for the earlier years.

Several serious criticisms of this curriculum have been voiced repeatedly. The first major criticism, which applies to algebra in particular, is that it presents inechanical processes and therefore forces the student to rely upon memorization rather than understanding.

The nature of such mechanical processes can readily be illustrated. Let us consider an arithmetical example. To add the fractions 5/4 and 2/3, that is, to ca1cu1ate

students are told to find first the least common denominator, that is, the smallest number into which 4 and 3divide evenly. This number is 12. One then divides 4 into 12, obtains 3, and mu1tiplies the numerator 5 of the first fraction by 3. Siniilarly one divides 3 into 12, obtains 4, and multiplies the numerator 2 of the second fraction by 4. The result thus far is to convert the above sum into the equal sum

A good teacher would no doubt do his best to help students grasp the rationale of this process, but on the whole the traditiona1 curricu1um does not pay much attention to understanding. It relies upon drill to get, students to do the process readily.

After students learn to add numerical fractions they face a new hurdle when asked in a1gebra to add fractions where letters are involved. Though the saime process is used to ca1cu1ate

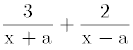
the individual steps are more complicated. Again the curriculum relies upon drill to put the lesson across. The students are asked to carry out the additions in nurmerous exercises until they can perform them readily

They are taught many dozens of such processes: factoring, solving equations in one and two unknowns, the uses of exponents, addition, subtraction, multiplication and division of polynomials, and operations with negatlve numbers and radicals such as \/3 in each case they are asked to imitate what the teacher and the text show them how to do. Hence the students are faced with a bewildering variety of processes which they repeat by rote in order to master them. The learning is almost always sheer memorization.

It is a1so true that the various processes are disconnected, at least as usually presented. They rarely have much to do with each other. While all these processes do contrìbute to the goal of enabling the student to perform a1gebraic operations in advaned mathematics, as far as the students can see the topics are unrelated. They are like pages torn from a hundred different books, no one of which conveys the life, meaning and spirit of mathematics. This presentation of algebra begins nowhere and ends nowhere.

After a year of such work in algebra the traditiona1 curriculum shifts to Euclidean geometry. Here mathematics sudden1y becomes deductive. That is, the text starts with definitions of the geometrìcai figures and with axioms or basic assertions which are presumably "obviously true" about the figures. They then prove theorems by applying deductive reasoning to the axioms. The theorems follow each other in a logical sequence; that is, the proofs of later theorems depend upon the conclusions already established in the earlier theorems. The sudden shift from mechanical algebra to deductive geometry certainly bothers most students. They have not thus far in their mathematics education learned what "proof" is and must master this concept in addition to learning subject matter proper.

The concept of proof is fundamnental in mathematics, and so in geometry the students have the opportunity to learn one of the great features of the subject. But since the final deductive proof of a theorem is usually the end result of a lot of guessing and experimenting and often depends on an ingenious scheme which permits proving the theorem in the proper logical sequence, the proof is not necessarily a natural one, that is, one which would suggest itself readily to the adolescnt mind. Moreover, the deductive argument gives no insight into the difficulties that were overcome in the original creation of the proof. Hence the student cannot see the rationale and he does the same thing in geometry that he does in algebra. He memorizes the proof.

Another problem troubles many students. Since algebra is also part of mathematics, why is deductive proof required in geometry but not in algebra? This problein becomes more pointed when students take intermediate algebra, usually after the geometry course, because there proof is again abandoned in favor of techniques.

With or without proof, the traditional method of teaching results in far too much of only one kind of learning - memorization. The claim that such a presentation teaches thinging is grossly exaggerated. By way of evidence, if evidence is needed, I have challenged hundreds of high school and college teachers to give open book examinations. This suggestion shocks them. But if we are really teaching thinking and not memorization, what could the students take from the books?

The traditiona1 curriculum has also become too traditional. Some topics that received considerable emphasis for generations have lost significance but are still retained. One example is the solution of triangies in trigonometry. Here, given some parts - sides and angles of a triangle, the theory shows how to.compute other parts and even how to use logarithms in the calcu1ations. This topic, which had far more relevance when trigonometry was taught primarily to prospective surveyors, should have been deemphasized long ago. Another example is the computation of irrational roots of polynomia1 equations. The method usually taught, called Horner's rnethod, requires several weeks of class tinre and does not warrant it.

There are also minor logical defects in the traditional currìcuium. For example, students are taught that x^2-4 can be factored into (x+2) (x-2), but that x^2-2 cannot be factored. However, the latter can be factored if we are willing to introduce irrational numbers. In this event the factors are x-\/2 and x +\/2 . Likewise x² + 4 can be factored if we are willing to use complex nurnbers. In this case the factors are x + 2i and x-2i

where i =\/-1 . Thus the error made in the traditional method of teaching is the failure to specify the class of numbers we are willing to consider in order to perform the factorìng.

Beyond the few defects we have already described, the traditional curriculum suflers from the gravest defect that one can charge to any curriculum - lack of motivation. Mathematics proper, to use the words of the famous twentieth-century mathematician Hermann Weyl, has the inhuman quality of starlight, brilliant and sharp, but cold. It is also abstract. It dea1s with mental concepts, though some, such as geometrical ones, can be visualized. On both accounts, the coldness and the abstractness, very few students are attracted to the subject.

Young people can no doubt see that there is some point to learning arithnretic but they can see little reason to study algebra, geometry and trigonometry. Why shou1d they learn the addition of algebraic fractions, the solution of equations, factoring and other topics? The appeal of geometry is not greater. It is true that students can see what geometry is about and what the theorems assert; the figures make clear what this branch of mathernatics dea1s with. But the question of why one should study this material is still not answered. One can readily understand what the history of China is about, but may still question why he shou1d be obliged to learn it.Why is it important to know that the opposite angles of a parallelogram are equal or that the altitudes of a triangle meet in a point?

Clearly one cannot defend algebra, geometry and trigonometry on the ground that they will be of use later in life. The educated layman does not have occasion to use this knowledge at any tinre unless he becomes a professional scientist, mathematician, or engineer. But this group cannot be more than a few per cent of the high school popu1ation. Moreover, even if all of the students were to use some mathematics later in life this usage cannot be motivation. Young people cannot be asked to take seriously material that they might need years later. This motivation is often described as offering "pie in the sky."

As a matter of fact, in an effort to motivate the students, the schools did try to teach some uses of arithmetic in the seventh and eighth grades. They taught simple and compound interest and discount on loans. But twelve- and thirteen-year-old students did not take to such material and the experinrent is conceded to be a failure. The motivation must appeal to the student at the time he takes the course.

Another motivation often dang1ed before students is that they must study mathematics to get into college. If the mathematics they have been taught in elementary and high school is typical of what lies ahead in college, they may not want to go to college.

The prospective mathematicians, scientists, and engineers will find mathematics useful in their careers. But if the mathematics presented gives no inkling of how it will be useful and if it is in itself totally unattractive, telling the students that it is needed in science and engineering wiIl only encourage them to seek another career.

Much of the mathematics taught is often defended as "training the mind." There may very well be some training, but the same effect can be achieved with subject matter that is far more understandable and agreeable. One could teach the commonly used forms of reasoning by resorting to social or simple legal problems whose relevance to life is far more apparent to the students. One does not need mathematics to teach people that the statement "All good cars are expensive" is not the same statement as "All expensive cars are good." Moreover, the use of social or legal problems does not require the mastery of technical language, symbolism, and abstract concepts, which tend to obscure the reasoning. Thus it is far more difficult for the student to see that the statement "All parallelograms are quadrilaterals" is not the same as "All quadrilaterals are parallelograms." In fact, experience in teaching shows that to make the logical arguments used in mathematical reasoning clear to the student, one must use non mathematical examples involving the same arguments. Moreover, there is some question about whether the training to think in one sphere carries over to thinking in another. One may be inclined to believe that it does, but one could not prove that this is so.

Another commonly advanced justiification for teaching mathematics at the high sohool level is the beauty of the subject. But we know that the subjects taught have not been selected because they are beautiful. They have been selected because they are necessary for further work in mathematics. There is no beauty in adding fractions, in the quadratic formula, or in the law of sines. No amount of preaching or rhapsodizíng about the beauty of mathematics will make such ug1y ducklings appealing. Moreover, novitiates - are not likely to find beauty in a subject they are still striving to master, any more than one who is learning French granrmar can appreciate the beauty in French literature.

A few students are attracted to mathematics by the intellectual challenge or because they like what they happen to do well. The rare student who experiences this challenge may indeed be intrigued - as some mathematicians are - by the fact that there are only five regular polyhedra. However, as far as most students are concerned, the world would be just as well off if there were an inifinite number of them. As a matter of fact, there is an infinite number of regular polygons and no one seems depressed by this fact.

There is indeed an intellectual value in mathematics. But there is a question of whether young people can appreciate it just as there is about whether a six-year-old can appreciate Beethovens music. If the teacher proves a theorem of mathematics, the student will still be struggling to understand the theorean, its proof and its meaning. While undergoing such struggles the student is not likely to be impressed with the intellectual content and what the human mind has accomplished. In him the theorem and proof produce bewilderment and confusion.

Beyond the purported values of training the mind, beauty and intellectual challenge, the defenders of the traditional curriculum point to the exercises. These, they say, show uses of mathematics and should convince the student that the material is important. There are work problems such as the ditch-digger's dilemma. "One man can dig - a ditch in two days and another in three days. How much time will be required if both men dig it together" Such problems create pointless work.

Then there are tank-filling problems for students who have no swimming pools to fill. Or the mixture problems: "How many quarts of milk with ten per cent cream and how many quarts of milk with five per cent cream must be mixed to make a hundred quarts of milk with fifty per cent cream?" Such problems are useful to farmers who wish to fake the cream content of their milk. Other mixture problems concern mixing brands of coffee or brands of tea to make undrinkable brews.

There are age problems too: "Jane is twenty years older than Mary. In ten years time Jane will be twice as old. How old is Mary?" This type of problem calls for finding out other people's ages, and many people are sensitive about their ages.

There are also number problems, such as "One number is three times another number minus two. What are the numbers?"(The numbers racket is actually illegal.) More realistic are board problems. "A board seven feet long is to be cut into two parts, one of which is to be two feet longer tban the other. How long are the parts?" Of course students are bored with board problems.

And we shouldnt neglect to mention the time, rate and distance problems, such as up- and down-river travel for students who are going nowhere and whose desire to go anywhere has not been aroused. Some problems involve taking walks around a circular garden and ask for the dimensions of the garden. If we allowed the students to take walks around the garden and provided each with a pleasant companion we wou1d do the stu-dents more good.

All these problems are hopelessly artificial and will not convince anyone that algebra is usefu1.

Some authors of algebra texts do point to "truly physical" problems. For example, Ohms law states that the voltage E equals the current I times the resistance R. In symbols E = IR. Calculate E if I = 20 and R = 30.
But the current involved in such problems doesnt drive any mental motors. So far as the student is informed, Ohms law could be describing the number of marriages in Burma each year.

For generations the calculus textbooks have asked students to calculate centers of gravity and moments of inertia of bodies without ever pointing out why these quantities are significant. Consequently, the gravity of these problems produces nothing but inertia in the students. Such physical problems, presented with no preliminary explanation of physical background or physica1 significance, mean nothing to the student. Clearly, a physical application is worthless if the student cannot see what is accomplished.

Even the use of the word "application" is often bothersome. Students are taught, say, a formula for area and are then asked to calculate areas with it. These calculations are supposed to be an application. This kind of application adds insult to injury. Since the so-called applications are still pointless and still part of mathematics proper, in what sense are they applications?

The fact is, then, that no motivation for the study of mathematics is offered in the traditiona1 curriculum. Students take it because they are required to. Motivation means more than a psychological stimulus. Genuine motivatîon also supplies insight into the very meaning of the mathematics. A great deal of mathematics, particularly on the elementary level, was suggested directly by real situations and problems. The bare formula s = 16t² acquires meaning when one learns that it relates the distance fallen and time of travel of an object which is dropped. An ellipse becomes more than just another curve when one learns that it is the path of a planet around the sun. Moreover, the questions that are raised about the formula and about the curve become meaningful because they concern the physical situations. The physical meanings also supply, in many cases at least, the power to think about the mathematical problems that are raised, because the mathematics is no more than a representation of the physics and a means of solving physical and other problems.

The failure to present the meaning of mathematics is analogous to teaching students how to read musical notation without allowing them to play the music. Students might be taught how to recognize full notes, half notes, sharps, flats, the key, and how to transpose music from one key to another without ever hearing any music. But if they do not hear what these various notations and techniques mean, they will be left with meaningless and boring skills.

The traditional curricu1um has been faithfully reproduced in thousands of textbooks. The strongest reaction induced by the traditionaltexts is that they are insufferably. dull. Most textbook writers seem to believe that scientific writing must be cold, spiritless, mechanical and dry. These books have no authors. They are not only printed by machines; they are written by macbines.

Textbook writers also seem to take inordinate pride in brevity, which can often be interpreted as incomprehensibility. Reasons for steps are either not given or given so briefly as to make the presentation almost useless to the student. Many authors seem to be saying, "I have learned this materia1 and now I defy you to learn it."Brevity in mathematical exposition is the soul of witlessness and obscurity.

The most disturbing fact about many traditional mathematics texts is that they lack originality and repeat each other endlessly. A few thousand arithmetic, algebra, geometry, and trigonometry texts have been published since 1900. Practically all of the texts on any one of these subjects contain the same materia1 and presentation; only the order of the topics is different.

But there is hope for progress because each contains at least ten topics, and the number of permutations of ten objects ten at a time is 3,628,800. It would be difficu1t to estimate how many trigonometry texts have been written with the justification that they treat the general angle before the acute angle. One can be sure, however, that just as many boast of treating the acute angle before the general angle. The only thing that is acute about these books is the pain they give the reader.

Are there no variations among these books? There are variations such as the elementary algebra and the advanced algebra, the elementary advanced algebra and the advanced elementary algebra, the half-course and the full course, the seven-eighths course, and so forth. Here, too, there is hope for "progress" because there are irrational numbers; hence, we can look forward to irrational algebra courses.

What is especia1ly disturbing about these books is that many of the authors are consciously dishonest to their profession. I asked one professor who had written "umpteen" trigonometries of the full and partially full type why he included such useless topics as the solution of oblique triangles by the law of tangents and the law of half-ang1es. He admitted that these topics are worthless, but said he included them because the books sell better. Apparent1y, no matter how many trigonometries a man may write, not even one can reflect his honest judgment.

I asked another professor, who published a stereotyped college a1gebra, why he bothered to write such repetitious nonsense. Oh, he said, I can write the stuff between classes without having to think about it. Why shouldnt I do it? Needless to say, no thinking was evident in the presentation of the material.

Another professor published a book which included some material that he believed to be unimportant. He admits this in his preface and then says quite candidly that he included this material with an eye to the niarket. Such honest dishonesty!

Those authors who repeat each others topics are in a sense plagiarizing. But the plagiarism extends beyond that. Paraphrases of whole sections of material covering many paragraphs are readily found. One author took whole chapters from another book with on1y minor changes, acknowledging, of course, the inspiration of God, Euclid, Newton, and Einstein.

Most traditiona1 mathematics textbooks appear to be commercial jobs that make a contribution only to the authors' pocketbooks. The ethics of some teachers, to say nothing of their mentalities, is evidently in a sad state. The only persons who can claim any credit for original work in connection with these books are the publishers' publicity men, who must think up good blurbs for the advertisements.

Fairness requires that one mention recent improvements in the format of mathematics texts. Important formulas are now enclosed in red boxes. Other texts use overlays of plastic to show the increasing complexity of a figure as one overlay after another is superimposed on the origina1 text figure.

Clearly the defects of the traditiona1 curriculum are numerous. The reliance upon memorization of processes and proofs, the disparate treatments of algebra and geometry, minor logical defects, the retention of a few outinoded topics, and the absence of any motivation or appeal explain why young people do not like the subject and therefore do not do well in it. Their dislike is intensified and their difficulties in understanding are compounded by being asked to read dull, poorly written, and commercially contrived textbooks.

Certainly reform was called for. The leaders of the new mathematlcs movement did not cite all of the above defects. However, they did point the finger at some of them. So let us look now at what these people proposed to do and try to evaluate their effectiveness in improving the teaching of matheinatics.

Professor Morris Kline

I am very grateful for the kind permission of Professor Kline's widow, Mrs Helen Kline for this book to be reproduced.