| [HomePage] | Prof Morris Kline | |
CHAPTER: 4 The Conflict Between Research and teaching
What a blessed place this would be if there were no
undergraduates!. . . No waste of good brains in
cramming bad ones.
Leslie Stephen
Note! [70],[71], etc. represent book page numbers.
[70]The major role of the universities is to carry on two functions - research and teaching. However, money and facilities are limited. The universities solve this problem by appointing research professors. Such people, they assert, advance knowledge and improve all levels of education directly and indirectly. More specifically they maintain that researchers are ipso facto good teachers. They also assert the converse: To be a good teacher one must be a good researcher. Hence appointment, promotion, tenure, and salary are based entirely on status in research.
Although there is justification for the insistence that professors who train future researchers be capable in research, for most of the teaching that the universities are, or should be, offering, the research professor is useless. There is in mathematics, and almost as surely in other disciplines, a direct conflict between teaching and research.
[71]One argument advanced in favor of the research man is that he has superior knowledge. But what knowledge does he possess? He is almost sure to be a specialist. The specialist is like a miner who never surveys a landscape but who digs a barely passable tunnel into a mine to research a small lode of gold that may in fact prove to be tin. Such research narrows rather than broadens. What the professor does in his research has little if any bearing on what he has to teach at the undergraduate and even beginning graduate levels. A specialist in some corner of abstract algebra may know nothing about non-Euclidean geometry. In fact, the creative researcher is most likely to be no more than a proficient but limited technician in one minuscule area. The irrelevance of specialized knowledge for teaching is not peculiar to mathematics. A professor of English who has specialized in philology or in the love life of Madame Bovary is not by virtue of this research equipped to teach elementary composition or a survey of literature.
Not all mathematical research is specialized. For example, some work on abstractions and generalizations is rather broad. But, apart from the worthlessness of much of this material (see Chapter 3), this work is far too sophisticated for most of the teaching professors are called upon to do. Abstractions and generalizations are meaningful only to students who already have a considerable knowledge of more concrete mathematics. unfortunately, researchers are prone to plunge at once into abstractions and generalizations because these are dear to their hearts.
The research professor's knowledge is of questionable value for another reason. Most mathematical research today is "pure"; it has no relevance to problems arising in the real world. But most of the students who take mathematics, about 95 percent, plan to be physical scientists, engineers, economists, actuaries, statisticians, and primary and secondary school [72] teachers. The typical researcher's knowledge is useless to such students.
Beyond all the previous reasons for devaluating the knowledge research professors possess, there is an additional one that applies specifically to mathematics education. Mathematical knowledge is cumulative. Just as algebra depends on arithmetic, the calculus on algebra, differential equations on the calculus, and so on, so the researcher's knowledge is accessible only to those who have considerable prerequisite knowledge in his area of research.
A common argument often advanced in favor of the researcher is that he evidently loves his subject and will communicate his enthusiasm to his students. One must recognize, however, that research today is - as Professor Truesdell, whom we have already cited, and Blaise Pascal much earlier, called it - far more a trade than a profession, and many people engage in it merely as one way to make a living. Indeed, since the universities stress research as the road to personal advancement, many professors are pressed into research much as draftees are pressed into the army whether or not they are willing to fight. Research is a highly competitive activity, not a labor of love. The pressure to publish is exemplified by the message one chairman sent to the members of his department: "A theorem a day means promotion and pay."
Even the enthusiastic professor who is deeply engrossed in his research almost unconsciously assumes that his mission is to stir up interest in his specialty, and accordingly rushes his students toward it at a pace they cannot maintain and at the expense of far more valuable and basic material. He seeks to train specialists even though this training is useless to almost all of his students.
Moreover, since prominence and visibility in his field is demanded, the professor undertakes activities that enable [73] him to shine. He will publicize his results at countless conferences and professional meetings. He will pursue grants and consulting arrangements that, beyond being profitable, aid his prestige. To attract attention he will seek office in a professional society. All these activities enhance his commercial value and further his personal advancement. What about obligations to students? This is the nethermost consideration. Even loyalty to his institution is not respected. Professors negotiate their own research grants and take them along when they transfer to another institution. In brief, they become denizens of the marketplace. Professors have no more conscience about obligations than has any other group chosen at random.
The layman tends to think of research as a genteel, leisurely activity, conducted with an open, disinterested attitude and devoted to the pursuit of truth. Actually it is a fierce battle for survival. Since priority in publication means everything, a researcher must push his work as fast as he can lest someone else beat him to it. Lord Ernest Rutherford, one of the greatest of British physicists, wrote in 1902,
"I have to keep going, as there are always people on my track. I have to publish my present work as rapidly as possible in order to keep in the race ...."
And the attempt to keep up with the literature in his field will absorb a considerable amount of a researcher's time and energy. The intensity of the competition even obliges researchers to adopt invidious practices more commonly attributed to the business world, such as refraining from telling others what they are trying to do or what partial success they may already have. For the sake of an immediate publication, a researcher may feel compelled to publish shoddy results, even though he may be quite sure that further efforts will produce a far better paper. Research requires an all-out effort and forces neglect or perfunctoriness in teaching.
[74]The universities' insistence on research imposes a special hardship on young Ph.D.'s They have just emerged from indoctrination in the purity of mathematics and from the dark recesses of some specialty they have pursued for two or three years. The doctorate conferred upon them is not the certification of a teacher but the official stamp of cultural deprivation. They then receive a three-year appointment during which they are expected to demonstrate their brilliance through publication. But this is just the period when most begin to teach; they must spend time in the preparation of courses that are new to them and in learning much about the art of teaching. After two years of service it is customary to notify these teachers whether their appointments will be renewed. Actually, not even two years can be used to demonstrate their research strength; the journals are overcrowded and many months must elapse before a paper is refereed and even accepted for publication. Since up to the time of their appointment these young teachers did only one piece of research, the thesis, and that was done under the guidance of a professor, they face a formidable task. Even if good teaching is regarded with some favor in their institutions, tyros in teaching certainly cannot expect to shine in this capacity. There is but one human response to such a conflict. It is publish, and perish the students.
The folly of expecting young Ph.D.'s to justify their claim to appointment or tenure through publication is evidenced by the case of Albert Einstein. After obtaining a diploma at the Zurich Polytechnic Institute, he sought merely an assistantship in a German university in order to obtain a doctor's degree. But at that time he had no publication to demonstrate his capacity for research. He therefore took a job as an examiner in the Swiss patent office at Berne. Several years later, in 1905, he published three brilliant [75] papers, including the one on the special theory of relativity. Six more years elapsed before he obtained his first university position at the German university in Prague.
The requirement of research from young Ph.D.'s was ridiculed recently by a professor of philosophy at an Ivy League institution: "Most of the great philosophers could not have gotten tenure at Blank University; they published their important work after they were forty. Kant didn't write anything for twelve years - he would have been out on his butt."
That young men and women are expected, however unreasonably, to show research strength is readily confirmed merely by glancing at employment advertisements in the professional journals. One prestigious university advertised for an assistant professor who would already have published work of high quality and would be expected to continue to be active in research. The applicant was also to present evidence of proved effectiveness in teaching at undergraduate and graduate levels. All this was required from a young man or woman who, if applying for an assistant professorship, would be a Ph.D. of, at most, two or three years' standing.
A not uncommon advertisement reads essentially as follows:
Wanted: Young Ph.D.'s, ranks of assistant professor and higher. Must have proven research ability. Vita must include publications. Apply to Prof. I.M. Noble, Superior Community College, Worthmore, Nevada. (Salaries readily augmented. Short drive to Las Vegas.)
One would think that department chairmen, who can be in close contact with their young Ph.D.'s, would be able to judge potential without requiring publication. But the ability to discern talent is rarer than ability to do research, and many chairmen do not possess it. They often consult a colleague, who may be equally incapable of judging, or an outside [76] specialist who may be biased. Moreover, young people are not likely to be known outside a limited academic circle.
The conflict between teaching and research becomes even more apparent when one considers the demands of teaching. Perhaps the first consideration is breadth of knowledge. Commerce students, prospective elementary and secondary school teachers, and social science students are now consumers of mathematics. Engineering and physical science students also need subject matter different from that for pure mathematicians. Just as it would be folly to require prospective dentists to learn Anglo-Saxon, so it is folly to require that prospective engineers learn the rigorous foundations of mathematics. Even on the graduate level most students are not preparing for mathematical research. The professor should know what material is important for them and fashion suitable courses. But the research mathematician cannot devote time to such matters and so teaches the material with which he is at ease.
What else does good teaching demand? Certainly it calls for knowing what backgrounds students bring to the class. Mathematics, at the lower levels especially, is a sequential subject, and a course must start where the prior education left off. To know what freshmen bring to college calls for knowing what the high schools teach. This is especially true today because the high schools have been changing curricula under the influence of new movements. But research professors will not trouble to find out what is being taught.
A good teacher gets to know his pupils. Some can be asked to tackle the more difficult problems or do additional work. The poorer ones should be called upon only for work commensurate with their backgrounds. If required to do what is beyond them they will become discouraged. The teacher should get to know his pupils so well that he could grade them without relying upon any examination, though [77] He may give one for other reasons.
Good teaching also requires catering to the students, psychological needs - giving encouragement to some, putting pressure to work on others and imparting confidence to those who have been defeated by poor teaching in their prior studies. A good teacher must have a knowledge of other psychological problems that beset students, provide advice on how to study, and offer the stimulus of personal contact. To effectively understand his students the teacher must also accommodate himself to the outlook of young people and be part of their world.
A recent study asked about two hundred college sophomores to write 250-word essays describing the greatest mathematics teacher they ever had and giving the reasons for their choices. The characteristic chosen by most students, 78 percent, was, "exhibits a genuine personal interest in students." The second highest-ranking characteristic, "conducts interesting classes," was mentioned by only 53 percent. The fifth-ranking characteristic, "knowing the subject," was named by only 34 percent. (This last figure may well be accounted for by the presumption that this attribute is something every student expects of his teacher and so many did not bother to name it.)
Teachers should constantly invite questions from their students. Some researchers are bothered by questions in class that cause them to depart from their prepared lectures or to look up something with which they do not wish to become involved. They prepare "perfect" lectures and regard interruptions as presumptuous or indicative of stupidity.
To present the material properly a good teacher must know how young people think. Can a particular abstract concept be presented successfully to freshmen or should its presentation be delayed until the junior year? Will a rigorous [78]approach to the calculus succeed with students who are beginning the subject? In preparing to teach a course the professor must choose the most suitable text from the dozens of available ones. This selection is time-consuming and calls for judging what students on any one level can handle. Even if a professor spends the time but is not judicious in his choice, he is likely to accept a text that is clear to him but, because of inadequate exposition, unduly burdens the student. He must also pursue and keep track of books and articles on ways of presenting ideas effectively.
Modifications in curricula, usually needed to meet either changing student backgrounds or the introduction of a new area of application, place an additional burden on the teacher. For example, the invention of computers and their constantly increasing use call for altering some courses to take advantage of the availability of these devices. Remedial work with entering college students, now a major problem, requires special courses. The design of new or modified courses is a task that the good teacher undertakes at the expense of considerable time.
A good teacher must be perceptive. He must know what difficulties students have in learning at their stage of the game. It is not sufficient that the professor "knows his stuff." Knowing his stuff too often means that he has forgotten or is oblivious of the obstacles young people encounter in learning elementary ideas. He may regard these as trivial and pass over them as though they did not exist. The alert teacher must also be able to recognize late bloomers and to appreciate that slow thinkers are not necessarily poor thinkers.
Finally, a crucial problem in teaching is motivating the students. It does not occur to many professors that other people with different tastes or perhaps a better sense of values may not like mathematics. Students want to know [79] why mathematics or a particular topic is significant, and not just that their professor likes it.
Even on the more advanced level, where the professor can count on his students having some inclination toward mathematics, presenting theorems without the proper motivation leaves a class with no more than a meaningless collection of theorems, proofs, and procedures. Most professors are interested in mathematics and so cannot appreciate that there is a need to motivate students. In fact, such professors prefer to teach students whose drive is already so well developed that they do not need additional motivation. A professor's greatest joy is the bright doctoral student - and professors love to boast about their bright students as though they made them bright.
Supplying effective motivation is time-consuming and calls for experimentation. It also requires breadth of knowledge that the research-oriented professor does not have and may be unwilling to acquire. The natural and historically valid motivation would be supplied by real, largely physical, problems. But because mathematics professors have abandoned the real world, the break from science has also affected pedagogy.
A good teacher will take a hand in college affairs. Counseling of students and service on faculty committees and the university senate (through which the faculty cooperates with the administration) are obligations of the entire faculty. But researchers do not deign to concern themselves with undergraduate or even graduate affairs that involve cooperation with other departments and the administration. Hence, the burden falls on the men and women who are primarily teachers, and the conscientious teacher does not shirk it.
In short, teaching is a specialty that can be pursued only by people with the willingness to master the art through [80] persistent devotion and experience. It undoubtedly calls for wholehearted and almost full-time effort.
All these considerations, which exhibit the vastly different demands of research and teaching, do not include another vital factor, namely, the personalities of researchers and teachers. A teacher must be able to communicate his knowledge. Do mathematics research professors have this ability? In general they are introspective and introverted; they do not feel at ease with people; they shy away from personal contacts. They like to concentrate on their thoughts. They choose mathematical research partly because mathematics per se does not pose the complex problems that are involved in dealing with human beings. To repeat Bertrand Russell's words, ?Remote from human passions, remote even from the pitiful facts of nature, the generations have created an ordered cosmos, where pure thought can dwell as in its natural home and where one, at least, of our nobler impulses can escape from the dreary exile of the actual world.? He also said in his autobiography that abstract thinking destroys our humanity and draws us into ourselves, and he confessed that he was drawn into mathematics ?because it is not human.? Mathematics, then, is a refuge. Research in many fields is a solitary occupation; in mathematics it is likely to be a haven for those with scanty spirit and interests. Would such individuals be likely to communicate successfully with students?
The good teacher must be dynamic, articulate, engaging, clear, warm, sympathetic with students, interested in people as much as in ideas, and even a good actor. He not only should have a lively personality but also must have the proper temperament. He must be interested in young people. Their problems, to some extent, must be his. The student who wants to be an English major and rebels at taking a required mathematics course has a case that to him, [81]at least, seems sound. It is the teacher's function to convince him of the value of that course for his life as an educated person.
There are many professors who, though they wish to be good teachers and approach the work seriously, apparently believe that the wish is the act. The wish may be father to the deed, but the conception, pregnancy, and labor are missing. These require perception, time, and energy devoted specifically to the requirements of good teaching. Much of this art must be learned from the students. To the extent that the students show comprehension, interest, even excitement, satisfaction, drive to learn more, and response to deliberately posed queries intended to stimulate thinking - to that extent the teaching is successful. But where and in what respects it is not must be observed by the teacher and modification be made to remedy defects. This is far more than even the more student-oriented research professors are willing to do, because they reserve most of their time, thought, and energy for their research.
Many researchers are kind, polite, and well-meaning. However, they are also unable to make contact with the students, and some are even afraid to face them. These professors are often quite conscientious. They prepare material carefully; they write it on the board meticulously, and the students spend their class time copying what the professors put there. Such research professors are apparently so unworldly that they have not heard of duplicating machines.
Researchers are usually credited with not only the specific talent that enables them to be creative but also with an underlying superior intelligence that enables them to judge wisely and perform superbly in every situation they may face. The question of whether there is a special talent for mathematics cannot be settled by any objective evidence. [82] One certainly must doubt whether there are mathematical genes. Insofar as opinion can answer the question of talent, most notable is the opinion of Richard Courant, who was head of the world's leading department of mathematics in pre-Hitler Germany, at Gottingen University, and who converted a nondescript department of mathematics in the United States into one of the country's leading departments, perhaps the leading one. No one knew more great mathematicians of our century, or knew them more intimately. When asked whether there is such a quality as mathematical talent, Courant replied, "There is no such thing." And then he added, "Rather than ask what special qualities mathematicians possess, you should ask, what do they lack that other human beings possess." Perhaps this response also answers the question of whether researchers possess superior intelligence.
Though some administrators might concede a conflict between research and teaching, they fall back on other arguments for insisting on research as the qualification for faculty status. Original research, they say, is the surest proof of intellectual distinction and the surest guarantee that intellectual activity will not cease. Leaving aside for the moment the problem of judging the quality of original research, we must ask what intellectual distinction has to do with teaching. A truly distinguished intellect may be so far above the level of the students he must teach that he will fail to understand their problems and needs, even if he possesses the willingness to do so.
As to original research being the surest guarantee that intellectual activity will not cease, many researchers fade out in their thirties and even more do so in their forties. And if they do, they will most likely be dispirited, depressed, and even sour. Unfortunately, we have no figures on how many researchers fade out nor on how their number might [83]compare with those who emphasize teaching and remain intellectually alive in all sorts of activities. Certainly some research men do burn out. The general belief, though its truth is not definitively established, is that science is a young man's game. As P.A.M. Dirac, a Nobel-prizewinner in theoretical physics, once said, partly in jest:
Age is, of course, a fever chill
that every physicist must fear.
He's better dead than living still
where once he's past his thirtieth year.
It is vital that professors keep intellectually alive but it need not be through research. There are other ways which we shall discuss later. Moreover, what does it. benefit the student if the research professor remains alert but, in view of the nature of modern research, he remains narrow?
Many administrators and chairmen argue that some standard for selection must be used, and since research can be measured whereas teaching cannot, it is better not to risk hiring people who are primarily teachers. The argument is false. We have already pointed out (Chapter 3) that it is almost impossible to secure competent judgment of the quality of research and that in fact most current research is worthless. Evaluation of research boils down to quantity of publication; the contents are irrelevant. As long as his peers accept it, a researcher can publish almost anything - and his peers do accept it, because they wish the same treatment. The chairmen and administrators who say that research can be measured whereas teaching cannot are really admitting to counting pages of publication. This measure is as sound as looking at a university?s total expenditures to determine whether it is fulfilling its role as an educational institution. One wonders how administrators would have judged the young Isaac Newton, who, after receiving criticism of a [84] paper he had published, vowed never to publish again. Surprisingly, even in large departments the research cannot be evaluated with assurance. Each person is a specialist in his own field and really knows little, if anything, about the work of his colleagues. Evaluation by committee is no more reliable. Anyone who has worked on committees knows that enlisting several people to share the burden results in each member of the committee expecting the others to do the work and no one contributing anything. Instead, friendship, partisanship, jealousies, favoritism toward one field of research rather than another, gossip, and scraps of information decide the issues. Many department chairmen or committees called upon for one reason or another to judge a faculty member write to specialists in the appropriate field. This recourse to peers is hardly likely to produce a fair judgment. We have already noted (Chapter 3) the defects of the refereeing process, and all of these apply as well to the judgment of published research by peers. Moreover, because fads do play a role, a sound researcher working in a field that has not become fashionable will get a poor rating. Mathematicians are no more discerning of or receptive to new ideas than are small-town politicians whose constituents seem happy with the status quo. The idols of the tribe are not desecrated with impunity.
Beyond judgment by a professor's own department, decisions on promotion and tenure, even if recommended by the department, must usually be approved by a faculty committee. In view of today's specialization of research, there may not be even one member on the committee who can understand the research he must judge. And so the faculty committee, too, falls back on quantity of publication.
How does one judge teaching? Students are possible judges. However, students are young and their mature evaluation may come years later. Moreover, students differ [85] in their needs and demands. The indifferent student may value just entertainment and will rate high a teacher who is only an actor. The mediocre but conscientious student will appreciate steady-going, clear presentations, but flashes of brilliance from the professor will pass him by or upset him. Such a student wants to know only what to do and how to do it. The really bright student, who can read for himself, wants mainly direction, deep insight, and perhaps challenging problems. Obviously, a typical class will contain all types of students and the professor will get a mixed rating. In P addition, students are influenced by the grades they get. Finally, if compelled to take a course in a subject they dislike, they are certainly going to be antipathetic to the teacher. Hence, evaluation by students, though it should not be ignored, cannot be the main basis for deciding on a teacher's effectiveness. Admittedly, teaching is difficult to evaluate, and good teaching takes many forms. The professor who stimulates and excites students to work for themselves - even when he does little to present the subject matter proper and is even unsystematic in doing so - is certainly a good teacher. The sober, careful expositor who helps students to master the material and gives them the confidence that they will do well, but presumes student drive, is another excellent type. Still another is the professor who may be a dud in the classroom but who builds close personal relationships with his students, spends hours with them on their individual needs, and gives each student the feeling that he has a friend and counselor.
A department chairman can do a great deal to evaluate a teacher. He can make it his business to have frequent discussions on what topics the professor chooses to teach in a given course and how he presents his course. The chairman can get to know a teacher's character and temperament, his [86]interest in teaching, his choice of texts, the kind of examinations he gives, and his availability to students. Teachers can themselves demonstrate expertise by writing a good text, an expository paper, or developing a better pedagogical approach to a topic.
However, there is no objective and certainly no quantitative measure of teaching ability. Judgment enters here as in the evaluation of research and as, in fact, in all the important decisions men are called upon to make. And administrators who are not qualified to exercise judgment should not be allowed to serve in positions where they will be required to do so. Around the turn of the century William James said that the social value of a college education was to be able to recognize a good man when you saw one. But this ability is not possessed by most administrators. To decide whether a teacher is good they ask him to supply letters of recommendation (usually written by those who are no better judges than the administrator), and they ask for a list of his publications. Despite the inescapable need for applying true judgment instead of resorting desperately and fruitlessly to quantitative data, many administrators are unwilling or fearful to apply it. Judgments may be wrong, but all one can expect of a good administrator is that he is right most of the time.
The saddest fact about the evaluation of teaching is that most administrators don't care whether a teacher is recognized as superb by colleagues and students. Teaching just does not count in the universities. Of course administrators deny this.
All things considered, the very nature and demands of research and teaching are so diverse, the personalities and abilities required so different, that only a rare individual with an abundance of energy can undertake to excel in both areas - at least during the same period of his life. Generally, good performance in teaching is in inverse proportion to efforts in research. Of course some research men may be willing to teach, but ability to do so is another matter. Their wisdom may be consumed in their research.
Though any attempt to compile statistics on the number of mathematicians who were or are both good researchers and good teachers would be a massive task with much room for misjudgment, it is significant that two of the three men commonly selected as the greatest mathematicians present relevant case histories. Newton was a professor at Cambridge University and was known to be a very poor teacher. At times no students at all attended his lectures, and of those who did attend, few understood him. The paucity of students did not disturb him, but he was almost paranoid in his concern to receive credit for his creations.
Though not a bad lecturer, Gauss did not care to teach and said so. In 1802 he wrote to the physician and amateur astronomer Wilhelm Olbers:
"I have a real aversion to teaching. For a professor of mathematics it consists of eternal work to just teach the ABC's of his science; of the few students who go on, most continue to gather a file of information and become only half-educated, whereas the rare gifted students will not allow themselves to be educated through lectures but instead learn by themselves. And through this thankless work the professor loses his precious time."
Gauss attracted only a few students to his lectures, whereas his colleague, Bernhard Friedrich Thibaut, who contributed very little to mathematics, had a hundred. Gauss gave the same lectures with very little variation, year after year.
The third of the 'greats,' Archimedes, was not a professor [88] and, moreover, lived at a time when education was conducted so differently that his case is irrelevant.
In recent years not many great researchers have expressed in print their attitude toward teaching. But Godfrey H. Hardy, one of Great Britain's leading professors in the first half of this century, did so in his A Mathematician'sApology. "I hate 'teaching'," he wrote, "and have had to do very little, such teaching as I have done having been almost entirely supervision of research; I love 'lecturing' and have lectured a great deal to extremely able classes; and I have always had plenty of leisure for the researches which have been the one great permanent happiness of my life." One understands why Hardy titled his book A Mathematician?s Apology.
In our own time the researcher's lack of interest in teaching is patent. When a university seeks to attract such a person, it offers not only money, but also a light teaching load - the lighter the better. The university officials know that researchers do not want to teach. Beyond the small number of teaching hours, the researcher is offered the privilege of devoting some of those hours to a course or seminar in his own specialty. Many researchers have said frankly, "Universities would be fine places if there were no students." Quite a few have expressed their contempt for undergraduate teaching and often can be heard at evening social gatherings to bemoan the fact that they must meet an undergraduate class the next morning. They sneer at the mere teacher and act condescendingly toward the students whom they regard as dull and unworthy of their attention. Such researchers may know the mathematical theory of ideals, but they are certainly not familiar with the ideals of teaching. They present familiar techniques mechanically, and when faced with the inevitable consequence that the students are bored and baffled, they criticize the students for lack of interest. Actually, it is the professors who are not [89] interested. By continuing to teach the same old techniques, they avoid thinking about how to present the material. Admittedly, there are also people engaged primarily in teaching who would be graded A only for the speed with which they can empty a classroom. A bad teacher is a small-scale disaster that wreaks havoc as long as he lives.
Some would claim that ego and approval of the peer group are factors favoring the pre-eminence of research. Darwin did say,"My love of natural science. . . has been much aided by the ambition to be esteemed by my fellow naturalists." Yes, scientists do love recognition by their peers, especially since the time of Pythagoras. For mathematicians the peers consist, reasonably enough of fellow mathematicians - a society conditioned by the universities to approve only research. If the peer group were encouraged to grant recognition to teaching it might in fact do so. In any case, ego and approval from the peer group need not impel a frenzied rush to publication. True ego would demand genuine accomplishment, even if the attainment of it were to take ten years.
In view of the conflicting demands of research and teaching, how can responsible men continue to affirm that research professors are automatically good teachers and that good teachers ought necessarily to be seriously involved in research. It is understandable that researchers cannot believe that they are not good teachers. It would hurt their pride; and they are proud to the extent of egotism. Moreover, since so many are naive about what lies outside their own research, they uncritically accept these tenets. They would be shocked if they were to request their students, at the end of a course, to answer a questionnaire asking them to check one of the following: The teaching in this course has been a) excellent, b) good, c) fair, d) poor, e) execrable. But their confidence in their teaching ability is so [90] firm that they do not see the need to question their own effectiveness.
One would think that chairmen of departments would be more responsive to their obligations to the students, but they are not. Since chairmen are anxious to show that they can build and maintain research strength, they favor researchers. Thus, the chairmen, too, sacrifice the students. Many chairmen prefer researchers because they know only research and with unconscious immodesty seek men in their own image. Teaching they do not understand and so they regard it as unimportant.
It is more surprising that administrators accept such crass doctrines without evidence. It is their responsibility to foster teaching and research, and they should know whether researchers can also supply the teaching needs of students. But the administrators of even a moderate-sized university are far removed from the activities of the individual departments, and so they are unable to judge the quality of the faculty, the reasonableness of the extent or quality of the offering, and the quality of the teaching, even if that should be a concern. They concentrate on budgets and maintenance of regulations. A good bookkeeper could do what many deans and vice-presidents do. University administrations are staffed largely with people who strive hard to perpetuate what they do not understand. In such matters as teaching and research they are naive and merely repeat what they have heard. These administrators, too, do not see the need to check their beliefs.
Many administrators who know that research is in direct conflict with teaching profess nevertheless that research is a prerequisite. Why? What these administrators really seek is prestige, and any measure that builds prestige is favored. Whereas fifty and more years ago they sought to obtain it by attracting socially elite students, in today's world the [91] medium is research. Since teaching can be appreciated only by students, whose opinions do not count in the adult world, teaching is not valued. Researchers, on the other hand, publish, and so their names and their university affiliations receive publicity. Because research is considered (certainly by those doing research) to be a mark of genius, it is accorded glory that reflects on the universities sponsoring it. It is the mink coat of the university world. Researchers win Nobel prizes, awards from professional societies, election to the National Academy of Science, and other such honors, and these, too, build up the prestige of the universities employing them. In The American University Professor Jacques Barzun mockingly suggests that universities have used the formula
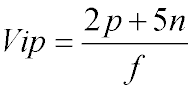
or Visible Prestige equals twice the number of Pulitzer prizes plus five times the number of Nobel prizes divided by the total number of faculty to measure their prestige. Of course this formula will not quite do for mathematicians; their work is not awarded Pulitzer or Nobel prizes.* However, election to the National Academy of Sciences or high office in a professional society may substitute for Nobels and Pulitzers in Barzun's formula. It matters not whether the honors are deserved (see Chapter 11); if the university can parade them in its literature, or if they receive five-line notices in the newspapers, that suffices. It apparently has not
*In an article in the New York Times Magazine section of November 21, 1976, Saul Bellow, winner of the Nobel Prize for Literature in 1976, quotes his wife, Alexandra, a professor at Northwestern University, to the effect that Nobel excluded mathematicians because his wife's lover was a mathematician.
[92] yet occurred to administrators that a more effective means of building prestige would be to hire a Madison Avenue advertising firm, but no doubt that soon will be done.
In their unbridled quest for prestige the universities do not rely solely upon researchers. The professor who heads a large project, such as space exploration, who travels frequently to Washington, or who receives newspaper attention for whatever he does is as desirable for faculty status as the most competent research man. So also are high government officials who can still in some way be named as faculty though they do nothing to further the legitimate activities of the universities.
There is ample evidence that universities seek prestige rather than quality. University Y has a fine mathematics department but nevertheless offers Professor A of University H a handsome salary to leave H and join Y. Now whatever good work A may be doing he can do just as well at H as at Y; hence the world does not benefit by the change in locale. But if A has prestige that will accrue to Y, that suffices for Y to invite him. Universities give all sorts of reasons for attracting people from other institutions. Of course, if A's subject is basic and there has been no one to teach it, or if a college decides to add graduate work and wishes to build a research faculty, the offer is justified. But these sensible reasons are much less frequently operative than the desire to acquire or enhance prestige. Universities hire professors the way some men choose wives - they want ones that others will admire.
The drive for prestige is evident almost everywhere. One university president making his maiden speech in that capacity to a group of faculty, alumni, and friends of the university opened his speech by mentioning the Nobelprizewinners, National Book Award winners, and other prominent figures who were members of the university staff. This opening was evidently intended to impress the [93] audience. At no time during the speech did the president mention any notable feature of the teaching function of the university. Ironically, this same university had reduced its retirement age to sixty-five and therefore, in effect, dismissed some very capable men and women, while continuing to appoint prestigious outsiders who were past sixty-five.
Why do the universities seek prestige? The main reason is money. Money has become the overriding concern of administrators. We have already noted that researchers attract government and private foundation money - which is then spent to attract more expensive researchers. Private universities also compete for students because tuition covers a substantial part of the universities? expenses,and students, often on their parents' urging, like to attend prestigious institutions. State universities compete for students so that they can demand more money from their legislatures. But there are intangibles also. Universities are run by individuals, and the prestige of the university enhances the individuals? standing. As Thorstein Veblen remarked many years ago, "Men of 'affairs' have taken over the pursuit of knowledge." Even professors, supposedly wholly devoted to their work, will accept a lower salary at a more prestigious university just to be more visible under the brighter radiance.
Though the craving for prestige is the motivating force behind most university actions, research is the socially approved word and, in fact, is one effective means of acquiring and maintaining prestige. Hence, the university administrators in their speeches and writings use the term "research" even when they are fully aware that it is a euphemism for what they really mean.
The universities' drive for prestige puts the professors in the anomalous position of being hired to teach, required to do research, and prized for the prestige they accord to the [94] university. The professors react accordingly. Even those who prove to be mediocre in research persist in trying to base their claim for advancement on research, partly because they know that this will count more than any other activity and partly because they are not convinced that their research is minor. They still hope to write the papers that will show their greatness and so are unwilling to devote appreciable effort to teaching and to university and departmental concerns. Others seek visibility in circles that university administrations prize, no matter what is sacrificed in the process.
The present qualifications for getting ahead in the professorial career are neatly summarized in the statistics of responses made in 1964 by members of the American Political Science Association:*
|
ATTRIBUTE |
RANK |
|
Volume of publication |
1 |
|
School at which doctorate was taken |
2 |
|
Having the right connections |
3 |
|
Ability to get research support |
4 |
|
Quality of publication |
5 |
|
Textbook authorship |
6 |
|
Luck or chance |
7 |
|
School of first full-time appointment |
8 |
|
Self-promotion ("brass") |
9 |
|
Teaching ability |
10 |
The inordinate emphasis on research is a relatively new phenomenon in American universities. We have related (Chapter 2) the fear expressed by Charles W. Eliot in 1869 that research would detract from teaching. Though Eliot may have exaggerated the danger in the late nineteenth century, inasmuch as research in the United States was then [95] in its infancy - and though he did later recognize that the universities must also support research - his fear ultimately proved to be justified.
*Sornit, Albert and Joseph Tannenbaum: American Political Science, Atherton Press, 1964.
Since the late 1940s the universities have demanded research and only research as the sole criterion for acceptability in the professorial career. This preference reminds one of G.K. Chesterton's remark, "My mother, drunk or sober." The mania for research has produced an invidious system of academic promotion, perversion of undergraduate education, and contempt for and flight from teaching. As Marshall McLuhan would say, the medium is truly the message, and the medium for university mathematics education is totally unsuited for the message. Or, as another professor put it at a recent meeting of the American Sociological Association, "Teaching represents the big vacuum in higher education."
I am very grateful for the kind permission of Professor Kline's widow, Mrs Helen Kline for this book to be reproduced.
Copyright © Helen M. Kline & Mark Alder 2000
Version: 21st December 2018
|