| [HomePage] | Prof Morris Kline | |
CHAPTER 8: The Misdirection of High School Education
Great God! I'd rather be
A pagan suckled in a creed outworn;
So might I,...
Have glimpses that would make me less forlorn;
William Wordsworth
[161] In a world in which changes take place with bewildering and discomfiting rapidity, mathematics education has provided one fixed landmark: the high school mathematics curriculum. This program is not only fixed; it is, thanks to the university ideology and practices that determine it, rigid and seemingly immovable. But the high school curriculum is certainly outmoded. Let us examine it.
The ninth grade is devoted to algebra and the subject matter has been almost entirely a series of disconnected, atomized processes, a mélange of topics: factoring, operations with polynomials such as x2+5x+b, operations with fractions such as (2x+5)/(3x+7), laws of exponents, and the solution of equations of various degrees and with one or more unknowns. This approach to mathematics proper is most unfortunate for, on the whole, algebra is a means rather [162] than an end. It is the spelling, grammar, and rhetoric of most mathematics, but it is not literature. If students of English were asked to spend years on preparation for reading - which is what the mathematics student does in eight years of arithmetic and the one year of algebra - without ever being introduced to the pleasures of reading, how would they react?
Beyond the fact that algebra per se is a means rather than an end, it involves a specific difficulty that bothers almost everyone - the use of letters. Just as number symbols are a hurdle for elementary school children, so literal symbols are a hurdle for high school students. To speak of 3x = 5 is not quite so terrifying as to speak of ax = b, wherein a and b are any numbers. In principle the idea is simple. Instead of talking about John and Mary, algebra talks about men and women. But generalizations about men and women are meaningful only to those who have had lots of experience with individual men and women. The analogue for algebra is lots of experience with various manipulations of numbers. Unfortunately, few students have more than a nodding acquaintance with arithmetic at the time they are propelled into algebra.
The use of literal coefficients did not occur to mathematicians until about 1600 A.D., roughly two thousand years after first-class mathematics had been produced by the Greeks. This fact in itself should warn teachers that students will balk at letters and that special devices are needed to make the transition from numbers to letters acceptable.
Whereas algebra proper is both meaningless and pointless, geometry, which students learn in the tenth grade, does have intuitive meaning. But the pointlessness is still glaring. Here, many dozens of theorems are proved in a logical sequence and, to the students, the goal seems to be to prove as many as possible. They are confined to learning inflexible [162] and obtuse trains of thought that permit no derailment. Just why anyone wants these theorems and how these theorems and their proofs were ever conceived is not treated.
The eleventh grade curriculum repeats the ninth grade subject matter because students did not learn that material, adds more algebraic processes, and introduces trigonometry - in which, among other topics, the students learn many identities at the risk of losing their own.
The twelfth grade contents, taken by relatively few students, has not been stable. But the material, whether solid geometry or the beginnings of calculus, is taught dogmatically and has been no more enlightening or enthralling than the preceding subjects.
How did this curriculum come about? It was fashioned in the nineteenth century by professors. In fact, as we have already seen (Chapter 2), the subjects that are now taught in the high schools were, in the United States, first taught only in the colleges. They were gradually moved down into the high school curriculum, but retained essentially the content that had been taught at the college level. During the years of transition, and even long afterward, committee after committee re-examined the curriculum. In detail the recommendations made by these committees did differ; some would teach factoring before exponents, and others the reverse. But in essence all agreed upon this traditional curriculum. The arguments they accepted in favor of it are hackneyed. The value of mental discipline was never questioned, and this purported value - that mathematics teaches thinking - freed the committees from any real concern whether the content was right. In addition, utility in daily life, preparation for college (after the subjects were transferred to the high school), and the learning of the higher truths in the noblest branch of our culture were also offered to justify the status quo. There seemed to be no doubt that [164] a2 - b2 = (a + b) (a - b) would uplift any soul.
There has been one change in recent years. The ineffectiveness of the traditional education, made more evident by the needs of World War II, stimulated some university professors to devote themselves to the reform of the curriculum. But these professors were even less informed about high school education than their predecessors of the last century or the early part of this century. Hence the reformers, too, thought in terms of the values usually claimed for mathematics education, such as preparation for the mathematics to be taken in college. Their contribution was to impose rigor, generalization, abstraction, and an emphasis on structure onto the traditional content. All the arguments marshaled against such features in preceding chapters apply with greater force to the high school curriculum, because the students have yet to find out what mathematics is all about.
Consider, for example, structure. Structure of what? The answer seems to be structure of abstract mathematical systems. It is true that the collection of positive and negative whole numbers and fractions - that is, the rational numbers - do have some properties that the whole numbers alone do not have. And the real numbers have the same structure as the rational numbers. Since these structures are all that high school students know, and not too clearly at that, what can the study of structure mean? One might as well ask students who have yet to see a dog to learn the structures of various species of animals. Moreover, what does structure mean in Euclidean geometry and trigonometry? The word is fashionable, but certainly not applicable to high school mathematics.
The new curriculum did not significantly alter the basic high school material. It secured the rigidity of the curriculum by adding rigor to the proofs and by burrowing deeper into[165] the foundations through set theory and symbolic logic. (See Chapter 6.) These "innovations" may have ensured the stability of the several mathematical edifices, but they also pulled the students so far down into the dark earth that they could no longer see the surface. Where light and air were needed, the new mathematics added steel beams. This reform, far from being an improvement, is more accurately described as a disaster. Fortunately, the new math is a passing aberration and there is no point to beating dead bones.
To the mathematician all of this standard material, whether in traditional or new math guise, is self-justifying; to the student it is self-condemning. The contents of all four years, certainly as presented, is abstract, dull, boring, and intrinsically meaningless. It consists at best, to use Alfred North Whitehead's phrase, of inert ideas. That students should have difficulty with it is inevitable. Psychologists found years ago that human beings could not remember more than six or so nonsense syllables one hour after they were memorized. If students haven't already acquired a dislike for mathematics in elementary school, the high school mathematics, particularly algebra, will surely engender it. The aftermath of traditional mathematics is revulsion. It is incredible that mathematicians and pedagogues could ever have believed and still do believe that this curriculum has any value. To be sure, one or two students in some classes do take to mathematics, either because they like it or because they wish to guarantee admission to college, but mathematicians would be the first to caution us that one swallow does not make a summer.
Let us review the arguments presented in defense of the traditional curriculum. One argument has been that this material is useful in later life. Does the average educated person use this knowledge in daily life? Do even mathematics [166] teachers, who know the subject, ever use the quadratic formula, the Pythagorean theorem, or the trigonometric identities outside of the classroom? The honest answer is no. Of course, the students learn that a straight line is the shortest distance between two points. That's useful. But even a donkey knows that: Put some food at a distance from him and watch the path he takes. The subject matter of high school mathematics - that is, the subject matter per se - is worthless knowledge. One or two topics, such as the calculation of compound interest, may prove useful. But the exceptions do not alter the general assessment.
And the high school courses have not taught thinking, pedagogues? assertions to the contrary. The traditional algebra teaches memorization of processes. Geometry purportedly emphasizes proof and therefore thinking; however, because the proofs are arranged in a logical sequence and this sequence is not natural, the rationale eludes the students and they are forced to memorize here, too. The students' appreciation of proof in geometry is epitomized in their oft-repeated remark that geometry is where you make proofs in two columns.
There is another frequently advanced argument for teaching mathematics: The subject is beautiful. Whereas in the college liberal arts course topics can be chosen for beauty, what is taught on the high school level is not notable for its aesthetic value. The choice of topics was based on what is needed for further education in mathematics. All the preaching and rhapsodizing will not make such ugly ducklings as factoring, adding fractions, and the quadratic formula attractive. Even the fact that the sum of the angles of a triangle is 180° is hardly attractive; a sum of 200° would at least be a round number.
Moreover, beauty is a matter of taste, and in the case of mathematics the appreciation of beauty calls for a certain [167] sophistication. It is in fact fortunate for society that not too many people are attracted by the esoteric beauty in mathematics. Our world would be sadly affected if even 10 percent of American high school students should decide that they wished to pursue mathematics for mathematics' sake. One good medical doctor is worth a thousand mathematicians who pursue mathematics for its beauty.
Omitted thus far is another value that champions of traditional mathematics cite: intellectual challenge. But should we sacrifice the 99 percent to the 1 percent who respond to this particular intellectual challenge?
The clinching argument that advocates of the traditional curriculum have used endlessly is that students need high school mathematics to go to college. It is inexplicable how anyone could take such a position in 1900, or even in 1930 when no more than 25 percent of the high school graduates went to college. Though the percentage has increased steadily, it is still true that no more than 50 percent of those who graduate from high school enter college. Moreover, at least 25 percent of those who start high school do not graduate.
Of those who go to college, at most 10 percent will need the techniques and theorems now taught in the high schools. The others either take no mathematics in college - many colleges no longer require a mathematics course for the bachelor's degree - or take a liberal arts course that does not use most of the currently taught high school mathematics. Do the colleges require the conventional high school mathematics for admission? They have not demanded it for many years. Some do not ask for any high school mathematics. Almost all of the others will accept any respectable two-year curriculum. Hence, one cannot justify the present high school curriculum on the ground that it prepares students for college.[168]
The argument concerning preparation for college has also been self-defeating. Faced with the dull traditional curriculum, fewer students have been taking academic mathematics. In 1928, when about three million students attended secondary school 27 percent took ninth-grade algebra and 18 percent took plane geometry. In 1934, the corresponding percentages for five and one-half million students had dropped to 19 and 12. Since 1934 the number of students attending secondary school has increased sharply, but the percentage taking academic mathematics has declined still more. Those who still take it do so only because most colleges, as already noted, require some courses, though the precise content is not restricted to the traditional subject matter.
Moreover, how appealing is the motivation - preparation for college - to the students? What normal fourteen-year-old really knows whether he is college bound? His parents may have definite plans, but these may go awry for many reasons. One certainly will be the child's reaction to high school work, and the traditional mathematics courses are not likely to induce a favorable reaction. Even at the time of graduation from high school, many youngsters are still uncertain about whether they will go to college. They often decide to do so only because of external pressures or circumstances. They may imitate what friends do or follow the path of least resistance.
To all of the arguments for the traditional high school mathematics curriculum the advocates of the new math added that our country's need for mathematically sophisticated manpower required the secondary school curriculum to bring students more quickly to the frontiers of research in pure and applied mathematics. In view of the sequential nature of mathematics, such an objective is preposterous.
Whether or not the values claimed for mathematics are [165] indeed present, certainly student readiness and capacity to appreciate these values should have entered into the considerations of the framers of the curriculum. The results of their failure to consider effectiveness have been notoriously poor. If we may judge by the results on the Scholastic Aptitude Tests, the performance of the best group - the college-bound - has been getting poorer year by year. More students are going on to college, but the high schools should be succeeding with all of these, at least. Additional evidence of ineffectiveness is the fact that remedial mathematics is now the biggest problem that the colleges face. In the two-year colleges 40 percent of the students taking mathematics are enrolled in remedial courses.
One cannot dismiss the traditional material without taking into account that some high school students will eventually use mathematics professionally. Since students at the high school stage do not know whether or not they will need mathematics later, everyone, so the argument goes, should be required to take it. However, only about 5 percent of the high school students will ever use mathematics and their needs should not dominate. They can be met in a manner that will be suggested later.
Is it, then, a mistake to require mathematics of all academic high school students? Not at all. The arguments against the teaching of mathematics are against the kind of mathematics that has been taught and against the justifications traditionally and currently given. At least in the United States, which is the only society that has sought to teach mathematics to all students, the vital material and the reasons for teaching it have been ignored entirely. The framers and reformers of the curriculum have approached the problem from the wrong direction. The values and objectives have been those that professors enjoy or respect. [165]
Before considering an alternative approach, let us note a critical distinction between elementary and high school mathematics education. Everyone has to know some arithmetic and a few elementary geometrical facts merely to get along in life. Arithmetic has basic practical value, much as reading and writing have. However, as we have already pointed out, this is not true of algebra, geometry, and the other high school subjects. Whereas we are obliged to present the elementary school material, we are freer to choose the material to be taught on the high school level. What are the objectives of an academic high school education? The courses in literature, history, science, economics, and foreign languages are intended to enable future adults to live more insightfully, wisely, and enjoyably. In short, they are an introduction to our culture. The mathematics courses should serve the same objectives. Hence, the mathematics we teach should be worth knowing for the rest of the lives of all students. It should contribute to a truly liberal arts education wherein students get to know not only what the subject is about but also what role it plays in our culture and our society. We must teach not just what mathematics is but what it does.
Teachers will undoubtedly ask, "Where and what is the material that constitutes a liberal arts curriculum?" To an extent we answered this question when we considered the contents of a freshman liberal arts course (Chapter 6). Admittedly, the intellectual level of the high school program and the background that it presumes must be taken into account. But there is a mass of suitable material, much of which can be culled from diverse sources. A few examples may convince doubting Thomases.
Elementary algebra deals with simple functions such as y = 5x, y = 3x2+6x, and the like. As purely mathematical expressions they are dull, devoid of interest; but they can be [171] and are used to represent an enormous variety of motions, the motions of balls, projectiles, rockets, and spaceships. Motion on the moon, which exhibits striking contrasts with motion on the earth, provides an exciting theme. The motion of objects dropped into water is another readily understandable and interesting phenomenon. Further exploration of simple functions leads to the law of gravitation, and to remarkable calculations such as the mass of the earth and the mass of the sun. Functions are not merely symbolic expressions; they are laws of the universe, and they encompass the behavior of grains of sand and the most distant stars.
Algebra can also be applied to the study of elementary statistics and probability. These techniques are used to obtain vital knowledge about the distribution of height, weight, intelligence, mortality, income, and other facts of interest and concern to every would-be educated person. The efficacy of medical treatments; the control of quality in production; and the prediction of future prices of commodities, population growth, and genetic traits such as susceptibility to diseases are achieved with the same tools. The reliability of conclusions reached on the basis of statistics and probability should also be taught. The well-known quip, "There are lies, damned lies, and statistics," should certainly be taken seriously in the study of statistics, because so many of the conclusions that are hurled at us are not supported by the data.
The uses of high school geometry are manifold. The determination of the size of the earth, the distances of the planets from the sun, and the periods of the planets; the explanation of eclipses of the sun and moon; and the calculation of inaccessible lengths, such as the height of a building, the width of a canyon, or the distance across a lake - all, though utilizing only the simplest geometry, are [172] remarkable feats.
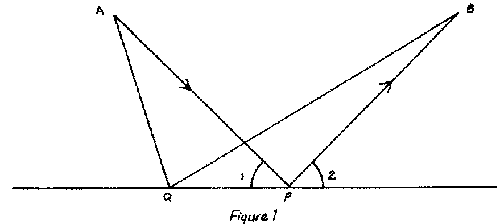
Equally accessible through geometry is the behavior of light. If a light ray travels from A to B (Figure 1) via reflection in a mirror, the path it takes, namely, the one for which angle 1 equals angle 2, is the shortest one it could possibly take. Thus the actual path APB is shorter than, for example, AQB. Moreover, since light travels in this situation with constant velocity, the shortest path requires the least time. In fact, in practically all situations light takes the path requiring the least time. Now light is surely inanimate. How, then, does it know to choose that path? Why does it seek "efficiency"? Here one can touch upon one of the grandest doctrines that man has proposed and in some centuries unquestionably affirmed. There is an order in nature, a design behind each phenomenon, and mathematical laws reveal and express that design. Who instituted that design? Perhaps best left unanswered, this question can be raised at the high school level.
A beginning can be made toward teaching the power of mathematical abstraction. What the pure geometry of the reflection of light says is that if one wants to go from point A to line QP and then to B, the shortest path is the one for which angle 1 equals angle 2. Suppose now that QP is a railroad track and a station is to be built to serve the people of towns [173] A and B. Where should the station be situated so that the total distance the people of A and B must travel to reach the station is a minimum? We have the answer. It is P. Suppose instead that a school or a telephone central is to be located along QP to serve towns A and B. Again, minimum distance or minimum telephone lines require that the school or central be placed at P. Thus, one geometrical theorem answers many different practical questions.
Other uses of elementary geometry can deal with a description of the functioning of our solar system, geography, perspective in painting, the structure of atoms and molecules, architecture, elementary engineering, surveying, navigation, and even clothes design.
If this cultural approach is extended to the third year of high school mathematics, wherein trigonometry is usually taught, many more values of mathematics can be demonstrated. When light travels from one medium to another, as from air to water, it changes direction; that is, it is refracted. The law of refraction can be simply stated in trigonometric terms. The importance of knowing this law is readily demonstrated because it is used in designing eyeglasses, and in understanding the functioning of the human eye and treating its diseases. The trigonometric functions enable man to analyze the pitch and quality of musical sounds, and this analysis is used in designing the telephone, radio, phonograph, and television. Of course, none of the above-mentioned applications calls for a knowledge of set theory. But teachers should be willing to make some sacrifices in behalf of 100 percent of the students.
That mathematicians of the past were inspired by real problems and found the meaning of mathematics through them is beyond dispute. Equally beyond dispute is that applications to real problems are a pedagogical necessity. However, there is some question about which applications[174] will be interesting and meaningful to students. Only experience will enable teachers to determine the best choices. Fortunately, the choices are so numerous and so varied, and interest in the real world is so much more widespread than interest in abstract mathematics, that attractive applications can surely be found. At the very least, it is easier to arouse curiosity about real problems than about mathematics.
Though authority can be found to defend almost any position, the words of some of the most famous educators of the past warrant reading. Friedrich Wilhelm Froebel (1782-1852), the founder of the kindergarten, stated:
Mathematical demonstrations came like halting messengers. . . . On the other hand, my attention was riveted by the study of gravitation, of force, of weight, which were living things to me, because of their evident relation to actual facts.
Aristotle asserted that there is nothing in the intellect that was not first in the senses. The use of real and, especially, physical problems serves not only to answer the question of what value mathematics has but also gives meaning to it. Negative numbers are not just inverses to positive integers under addition; they are the number of degrees below zero on a thermometer. The ellipse is not just a peculiar curve; it is the path of planets and comets. Functions are not sets of ordered pairs; they are relationships between real variables such as the height and time of flight of a ball thrown into the air, the distance of a planet from the sun at various times of the year, and the population of a country over some period of years. To rob the concepts of their meaning is to keep the bra nches of a fruit tree and throw away the fruit.
There is another value to be derived from developing mathematics from real situations. One of the greatest [175] difficulties that students encounter in mathematics is solving verbal problems. They do not know how to translate the verbal information into mathematical form. Under the usual sterile presentations in the traditional and new mathematics curricula, this difficulty is to be expected. On the other hand, if mathematics is not just applied to the real world but is drawn from the real world, as happened historically, its applicability is no longer a mysterious process. The difficulty students now experience in applying mathematics to real problems is very much the difficulty a French youth, who knows only French, would have in translating his thoughts into English. If, however, he is brought up in a bilingual region as are, for example, the French Canadians, he can certainly express himself in both languages.
The inclusion of applications offers still another advantage. As we have noted, most of mathematics arose in response to the desire or need to solve real problems. As the teacher treats such problems, he can include an account of the historical background in which the problems were tackled and even include some biography of the men involved. If skillfully interwoven, rather than added as disconnected appendages, the history and biography will not only enliven the courses but also will teach an equally important lesson: Mathematics is produced by human beings responding to a variety of problems. It is a living body of ideas that developed over the centuries and grows continually.
The defenders of the traditional material often rejoin that they do teach applications. Let us look at just a few of them. There are work problems such as the ditch digger's dilemma: "One man can dig a ditch in two days and another in three days. How much time will be required if both men dig it together?" Such problems create pointless work. Then there are tank-filling problems for students who have no [176] swimming pools to fill. And there are the mixture problems:
"How many quarts of milk with 10 percent cream and how many quarts of milk with 5 percent cream must be mixed to make one hundred quarts of milk with 50 percent cream?"
Such problems are perhaps most useful to farmers who wish to fake the cream content of their milk.
And we shouldn't neglect to mention the time, rate, and distance problems, such as up - and downriver travel, for students whose desire to go anywhere except out of the classroom will not be aroused.
Some authors of algebra texts point to "truly physical" problems. For example, Ohm's law states that the voltage E equals the current I times the resistance R. In symbols E = IR. Calculate E if 1 = 20 and R = 30. But if the concepts and the use of the law are not explained to the students, the current doesn't drive any mental motors.
The proposal that the first two or three years of secondary mathematics contain all sorts of genuine applications may seem radical, but a little perspective may correct this impression. In the seventeenth century mathematics courses comprised astronomy, music, surveying, measurement, perspective drawing, the design of optical instruments, architecture, and the design of fortifications and machines. In the intervening centuries some of these topics lost importance and were dropped from the mathematics curriculum. The expansion of mathematics itself and of knowledge generally has compelled educators to drop other topics. But the isolation of mathematics from all applications relevant to our times cannot be tolerated, even if the inclusion of applications necessitates covering less mathematical topography.
Beyond the demands of pedagogy, we must recognize that mathematics did not develop independently of other human activities and interests. If we are compelled for [177] practical reasons to separate learning into mathematics, science, history, and other subjects, let us recognize that this separation is artificial. Each subject is an approach to knowledge, and any mixing or overlap, where convenient and pedagogically useful, is to be welcomed.
The need to relate mathematics to our culture has been stressed by Alfred North Whitehead, one of the most profound philosophers of our age, and a man capable of the most exacting abstract thought. In his essay The Aims of Education, written in 1912, Whitehead says:
In scientific training, the first thing to do with an idea is to prove it. But allow me for one moment to extend the meaning of "prove"; I mean - to prove its worth.. . . The solution which I am urging, is to eradicate the fatal disconnection of subjects which kills the vitality of our modern curriculum. There is only one subject-matter for education, and that is Life in all its manifestations. Instead of this single unity, we offer children Algebra, from which nothing follows; Geometry, from which nothing follows. . . . Our course of instruction should be planned to illustrate simply a succession of ideas of obvious importance.
In another essay of 1912, Mathematics and Liberal Education (published in his Essays in Science and philosophy), Whitehead goes further:
Elementary mathematics. . . must be purged of every element which can only be justified by reference to a more prolonged course of study....
[T]he elements of mathematics should be treated as the study of a set of fundamental ideas, the importance of which the student can immediately appreciate; every proposition and method which cannot pass this test, however important for a more advanced study, should be ruthlessly cut out.... [s]implify the details and [178] emphasize the important principles and applications.
In 1912 Whitehead was addressing himself to essentially the same curriculum that we teach today. The criticisms and positive recommendations still apply and, in fact, with all the more force because the high schools now teach a more diverse group.
To present mathematics as a liberal arts subject requires a radical shift in point of view. The traditional approach presents those topics of algebra, geometry, intermediate algebra, and trigonometry that are necessary to further students' progress in mathematics per se. The new approach would present what is interesting, enlightening, and culturally significant, with the inclusion of only those concepts and techniques that will serve to further the liberal arts objective. No technique for the sake of technique should be presented in the first two or three years. In other words, the material should be objective-oriented rather than subject-oriented.
But what do we do for the future professional user of mathematics? Admittedly a small but appreciable percentage of the students will become mathematicians, physicists, chemists, engineers, social scientists, technicians, statisticians, actuaries, and other specialists whose work requires mathematics. Of course these students, too, should know the cultural significance of mathematics. Moreover, students who are already inclined toward a specific career will certainly take an interest in mathematics if they see how the subject is involved.
But if by pursuing the cultural objective we do curtail somewhat the technical preparation of those students who will need mathematics later, what can we do for them? Those who are convinced by the end of the eleventh year of schooling that they do wish to pursue mathematics for some [179] professional use should be offered an optional technical course in the twelfth year. Because these students know that the career they intend to follow will require mathematics, they will be better motivated and, most likely, quite capable of rapid progress. They should be able in one year to acquire a considerable technical background that might well include far more than they may acquire in the present traditional curriculum. In fact, these students, mixed in at present with indifferent or poorly prepared high school students, don?t go far in the ninth and tenth grades, and in the usual eleventh-grade class they are bored by repetition intended for the poorer students.
Beyond content there are many pedagogical considerations - such as the treatment of proof; getting students to enter into the discovery of results; the use of laboratory materials, among which for present purposes we may include the computer; and testing. However, these pedagogical problems lie beyond our present concern. Our discussion of content may be sufficient to indicate that all is not well in high school education.
More relevant, in view of the notoriously poor results of mathematics education, is the question of why the basic content of the high school mathematics curriculum has remained fixed. The answer is that for many generations the mathematics departments of the universities and of most four-year colleges have taught the same subject matter to all prospective high school mathematics teachers. In fact, on the whole, the prospective teachers are taught the same subject matter that is taught to all mathematics students. The professors project their own values and interests; in the present case, in which courses are directed to prospective high school teachers, student needs do not count. To study the problems of high school education and to fashion courses that would enable prospective teachers to meet those [179] problems would call for the full-time efforts of at least one professor in each college or university department. But the archenemy of all undergraduate education - the pressure to do research - precludes such attention. Though the professors of the schools or departments of education do teach prospective teachers how to teach, they are unable to counter the domination of content by the academic departments. Hence, their impact on curriculum is nil.
Consequently, the high school teacher is limited in knowledge and restricted to goals and values set by mathematics professors and administrators. However much he may sense the poverty of the material he is teaching, he has neither the expertise nor the power to change the curriculum.
Also, unsurprisingly, curriculum reform is not often welcomed by older teachers. Indoctrinated only in traditional, isolated, unmotivated mathematics, the teacher confronted with the challenge to teach more meaningful and more purposive material shrinks back in fear. When asked, for example, to teach applications involving acceleration, he throws up his hands and argues that the concept is too difficult for the students or that it presupposes a knowledge of physics. However the students and the teachers ride in automobiles. To get a car moving and to stop it one must accelerate or decelerate. A moving automobile rarely travels at a constant speed but accelerates and decelerates constantly; hence, the notion is certainly intuitively familiar. The students, who are still young and open to ideas, would not find the concept difficult - nor would the teachers, had they not been conditioned to concentrate solely on mathematics. In fact, it is even vital to teach acceleration. It is too rapid deceleration that causes many passengers in automobiles to go through the windshield. To require [181] teachers to teach applications does not impose any real hardship. Actually, very little knowledge of science is required to teach applications of high school mathematics; every teacher can acquire it. Prospective mathematics teachers should certainly study some science during their undergraduate days.
A rich, vital, and attractive high school curriculum can be fashioned. Reform should be led by experienced, knowledgeable, broadly educated professors. Specialists might serve as consultants but certainly should not lead. It would be equally important to have cultured nonmathematicians participate. Their judgment as to what the future citizen would find valuable should take precedence over that of the specialists.
High school mathematics that consists of algebraic techniques, proofs of geometrical theorems, and mazes of abstract concepts and symbols will continue to reduce the students to a state of bafflement and loathing. At present, many conclude that they do not have mathematical minds when, in fact, they have not had informative, inspiring, and stimulating mathematics education. Though sincere teachers have been imparting what they themselves have learned - skills and proofs - unconsciously and sometimes consciously they work hocus-pocus on their students, presenting and repeating opaque formulas, sometimes to the admiration but almost always to the bewilderment of their charges.
The current high school curriculum is a threat to the life of mathematics. If the schools do not offer a more rewarding and meaningful curriculum, then rather few students will take mathematics. Requirement for admission to college, which is the main factor keeping academic mathematics alive in the secondary schools, may not sustain high school [182] mathematics in the future. Almost certainly, it will cease to be a requirement. If high school mathematics is not made more attractive and significant to the student, mathematics as an integral part of general education will die quietly and its soul will rise to heaven through an atmosphere of irrelevance.
I am very grateful for the kind permission of Professor Kline's widow, Mrs Helen Kline for this book to be reproduced.
Copyright © Helen M. Kline & Mark Alder 2000
Version: 21st December 2018
|