CHAPTER 9: Some Light at the Beginning of the Tunnel

CHAPTER 9: Some Light at the Beginning of the Tunnel: Elementary Education.

I had been to school.. . and could say the multiplication table up to 6 x 7 = 35, and I don't reckon I could ever get any further than that if I was to live forever. I don't take no stock in mathematics, anyway.

Mark Twain (Huckleberry Finn)

[183] Of all the levels of mathematics education, from elementary to graduate, the elementary is the most difficult to teach. The primary reason is that we do not know enough about how young children learn. We know little more about how older children learn, but they are no longer as much dependent on the teachers.

In view of the lack of any sound knowledge of pedagogy it is not surprising that from the very founding of primary schools in the United States until about 1950, sheer ignorance determined the method of teaching arithmetic- drill in skills. Certainly, in the nineteenth century and prior to that there were no knowledgeable professors to train elementary school teachers and, in fact, most were trained in normal schools, which could hardly be considered college-level institutions. However, even when the training of elementary school teachers was taken over by the liberal arts colleges[184] and the schools of education, no improvement was made. The liberal arts professors were really not concerned about the mathematics that should be taught to prospective elementary school teachers, and the professors in the schools of education knew no more about how to teach than did their predecessors in the normal schools.

Educational psychology was introduced early in this century as a formal discipline in the schools of education, and prospective teachers were required to take a course in this subject. But the professors had nothing to offer. They endorsed and even applauded rote learning. The leader of this school of thought, Professor Edward L. Thorndike, maintained, as we noted elsewhere (Chapter 2), that students should be taught to respond automatically to any given question or problem. Repetition of the stimulus-response would develop skills. In fact, Thorndike maintained, in The Psychology of Arithmetic (1924):

Reasoning is not a radically different sort of force operating against habit but the organization and cooperation of many habits, thinking facts together. Almost everything in arithmetic should be taught as a habit that has connections with habits already acquired and will work in an organization with other habits to come. The use of this organized hierarchy of habits to solve novel problems is reasoning.

The value of this methodology can readily be tested. One has only to ask an educated adult, How much is 3/4 divided by 2/3? Inexplicably, teachers continued to demand rote learning in accordance with Thorndike's psychology while at the same time advocating the values of mental discipline and transfer of training in reasoning to other fields.

A new era was inaugurated in the 1950s when mathematics professors decided that the elementary- and secondaryschool curricula needed reform. Arithmetic became an [185] abstract, logically developed subject. To present this new approach teachers had to be trained or retrained. And so new courses in content were offered by mathematics departments.

Because set theory had been introduced as a topic to be taught to elementary school students, prospective teachers had to be taught set theory. The ludicrousness of what was and is, in the main, still taught may be illustrated by the attention given to the empty set, usually denoted by 4). Thus, if no apples are present, the emptyset of apples is denoted by 4). Some texts for teachers ask the students to name several different empty sets. Others ask them to prove that the empty set is unique. Further, there is strictly a logical distinction between an object and set of objects. A set or collection of books is not a book. Likewise, there is a distinction between the empty set and the set containing the empty set.

More generally, these newer courses stressed the deductive structure of mathematics, which means proof made by deductive reasoning from axioms. Presumably, without such proof nothing can be asserted. But in the elementary school deductive proof should play little, if any, role. Inductive arguments, physical evidence, measurement, and pictures are the basis for learning and understanding. However, the prospective elementary schoolteacher, sitting at the feet of a distinguished professor, is in no position to reject or refute his teachings. Hence when the student becomes a teacher he feels like a traitor if he induces young children to accept a process or technique on the basis of, say, pictorial evidence rather than deductive proof.

If the material just described is the best that mathematics[186] departments can offer prospective elementary school teachers, then they should offer no courses in academic mathematics to these students.

One defense of such college courses is that teachers must prepare children for the uses that will be made of mathematics twenty and thirty years from now. The professors also argue that understanding of fundamental principles will narrow the gap between elementary and advanced knowledge. Just what these future uses and advanced mathematics have to do with the education of children is not treated.

The content, then, of the courses usually addressed to prospective elementary school teachers is decidedly poor. To make matters worse, the teaching of such courses is often entrusted to graduate students or young instructors on the ground that the subject matter is simple and does not require the mastery of mathematics that the older professors have. The real reason is that the professors don?t wish to bother with courses for nonmathematicians.

The psychologists hastened to defend the new approach. Jerome Bruner's statement, in The Process of Learning,

"We begin with the hypothesis that every subject can be taught effectively and in some intellectually honest form to any child at any stage of development,"

has been quoted endlessly and used - in particular by the proponents of the New Mathematics - to defend teaching abstractions. The saving feature of this statement is its vagueness. What is an intellectually honest form of teaching Immanuel Kant's Critique of Pure Reason to six-year-olds'

It seems fair to say that most parents can discern as much about how children learn as psychologists have taught us. That all people, children in particular, must be amply grounded in concrete experiences before they can appreciate an abstraction is readily observed. That children differ[187] in the interest they take in learning, in the rate of learning concrete material, and in the ages at which they can grasp even simple abstractions, whether these differences are genetic or conditioned, is obvious.

With or without help from psychologists we can readily appreciate that the hardest part of any subject is the beginning, because it is strange. It is also the most important part, because the patterns of thought and the attitudes acquired at this time become established in young minds and then are hard to change. The obstacles to the learning of arithmetic are especially formidable. The first is that it deals almost immediately with abstractions. The number 5 is a meaningless symbol to most five-year-olds. More difficult is the question, Is 7 greater than 5? One might as well ask a child to calculate the distance to the star Sirius. Moreover, the abstractions become more remote from experience in the higher grade levels. Negative numbers are far more difficult to grasp and eluded the best mathematicians for over one thousand years after they were introduced.

Another obstacle to the learning of arithmetic stems from our ingenious but unnatural way of expressing quantity. Our number system uses positional notation; the two "l"s' in 151 have entirely different meanings. The sophistication of positional notation is evident from the fact that of the many civilizations that developed some system of arithmetic, only one, the Babylonian, conceived that scheme. The Europeans learned the idea from the Babylonians, and improved the scheme somewhat by shifting to base ten from base sixty. Though positional notation facilitates the operations of arithmetic, it makes comprehension more difficult. The rationale of long division is not readily understood and the usual square root process is even more difficult to comprehend. The elementary school teacher is obliged, if he is to avoid mindless drill, to apportion his efforts and the[188] available time between teaching skills and imparting understanding. Neither task is easy.

Still another difficulty is the precision of the language that must be employed. In ordinary discourse many ambiguities are tolerated and the meaning is usually deciphered from the context. Thus, a person who addresses a letter "Dear John and Mary" surely means that John and Mary are both dear to him, but grammatically the "Dear" modifies only John, or at least it can be so interpreted. Likewise, the banks that advertise that they are happy to extend small car loans are not specific as to whether they mean that they will make loans only on small cars or that loans on any cars would be small. Such ambiguities cannot be tolerated in mathematics; thus 10 - 7 + 3 is not the same as 10 - (7 + 3); if the latter is intended, the parentheses are essential. Likewise, 3 x 4 + 5 is intended to mean (3 x 4) + 5 and not 3(4 + 5). (Parentheses would, in fact, help; instead, elementary school students are taught that the strong operations - multiplication and division - must precede the weak operations of addition and subtraction.) Mathematical language must be precise even though it necessitates symbolism and stiltedness.

The difficulties we have described cannot be evaded. In contrast to the situation at the secondary-school level, there can be little choice of contents in elementary school mathematics. Every adult must be able to perform arithmetic and use common geometrical formulas for area, perimeter, and volume; and in our society some knowledge of statistics and probability is almost as imperative. Whether these last two topics should be taught in the elementary school or reserved for the secondary school is debatable.

In view of the content and the few principles we do possess about how children learn, what should prospective elementary school teachers be taught? A truly cultural liberal arts course, such as was described earlier (Chapter 6), would indeed be more helpful in the education of all people and [189] certainly to teachers of elementary mathematics. To the latter it would give some perspective on the place of mathematics in human affairs. Some of the knowledge gained could even be utilized in their teaching. But the primary need of prospective elementary school teachers is re-education in arithmetic. They know no more than they learned in elementary school and it is commonly conceded that these teachers, like most adults, are insecure in that knowledge. Many even dread the period that they must devote to the subject. These failings seriously hinder effective teaching. Re-education would certainly help, particularly because as college students these prospective teachers are more motivated than they were as elementary school students. Beyond re-education, the eoursç could give insight into arithmetic and geometry, which would fulfill the essential requirement that a teacher must know more than he teaches. Thus, whereas positional notation in bases other than ten should not be taught to elementary school students, it should be taught to prospective teachers. The usual square root process cannot be made entirely clear to children, but it can be to teachers. Terminology such as inverse, commutative, associative, and the like can be taught to prospective teachers, though it should not be imposed on youngsters. Since the elements of statistics and probability are entering the elementary school curriculum, certainly future teachers should know more about these topics than they will teach.

No doubt mathematics professors will object that such a course is not college level and will resent having to use their precious time and energy to teach such simple material. But the farce of teaching the kind of course they do give and their ignorance of the needs of elementary school teachers do not seem to trouble them. Apparently, bewildering students with endless questions on the empty set is college level.

Despite the at present poor preparation of elementary school teachers, some progress in elementary education has[190] taken place in the last few years, especially in the lower grades, whereas none is noticeable at the other levels. One reason may be reaction to the New Math. Of course, the New Math was a disaster at both the elementary and secondary levels, but the extent of the disaster was more evident at the primary school level. When students could not add 9 and 8, almost everyone was shocked. That a high school student could not solve x + 3 = 7 should have been equally shocking, but since solution of this problem is not required in daily life and is beyond most adults anyway, the failure to master simple algebra was not attacked as severely.

In any case, teachers concerned with the elementary school seem at last to have learned the obvious. Abstractions, however simple, acquire meaning only in terms of a host of concrete experiences. Thus, texts of the last few years have pictures of people, animals, houses, candy, and other objects familiar to children, and the whole numbers and operations with whole numbers are discussed for a long time only in connection with these pictures. That is no longer based on the commutative law or taught by pure rote.

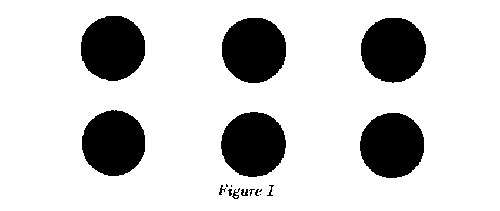
Children are asked to look at a rectangular array of discs (Figure 1) and they see that two rows of three discs and three columns of two discs still total six. They soon recognize that [191] the order in which any two numbers are multiplied is immaterial and thus learn the commutative property of multiplication. Fractions are parts of pies and it is visually obvious that 2/6 of a pie is the same as 1/3 of a pie. The student then readily understands the principle that one can multiply the numerator and denominator of a fraction by the same number and not change the value of the fraction itself.

Building up arithmetic on the basis of real situations accomplishes more than the teaching of skills. If a child learns to perform the four operations but has not constantly associated them with real problems, he will be in the position of not knowing which operation to use in a given instance.

As the teaching of arithmetic progresses to the higher grades, wherein operations with large numbers, more complicated fractions, decimals, and percentage are the topics, teachers, poorly prepared in their college education, often ask, What real phenomena or situations can we employ to make the arithmetic meaningful and purposeful? Some suitable themes are the same as those suggested for the first two years of high school, but the questions raised would be simpler. For example, given the speed of sound in air, students could be asked how far sound travels in a stated number of seconds or how long it takes a sound signal to travel a given distance. These questions are not intrinFically exciting, but one can readily introduce some that are. Sound travels at about 5,500 feet per second through the earth but at only 1,100 feet per second through air. Hence, a distant sound reaches the auditor more quickly through the ground. This is why Indians put their ears to the ground to hear a rider on horseback sooner. One can ask for the difference in time if the distance is one mile. Another application of the speed of sound uses the interval of time required for a sound to [192] reach a mountain and for the echo to return to calculate the distance to the mountain. The same principle is used to determine the depth of the ocean and of harbors, and to determine the distance of one submarine from another.

Work with the speed of light, which is 186,000 miles per second, can also lead to some novel facts. Given the distance from the earth to the sun how long does it take light from the sun to reach us? A calculation would show that it takes light from the sun eight minutes to reach the earth. Having learned this, students might be asked, Do we see the sun where it is now? Of course not. We see where it was eight minutes ago. It may have exploded in the meantime.

Speed, time, and distance can be applied to problems of sports. For example, a line drive - that is, a ball batted to follow practically a straight-line path - has a speed of, say, 100 feet per second and is fielded by an outfielder 350 feet from the batter. How many seconds does the outfielder have to get into position to catch the ball? A man on third base can run the 90 feet to home plate at 40 feet per second. A pitcher 65 feet from home can throw the ball to the catcher at a speed of 20 feet per second. Will the runner beat the ball to home plate? How many feet per second does a runner travel if he can cover a mile in 4 minutes?

The distinction between mass and weight can be made and utilized in elementary school work. In daily life we confuse mass and weight and the confusion does no harm. But in these days of space exploration the distinction is important, and it is easily taught. Mass, roughly speaking, is quantity of matter. Weight is the pull that the earth or some other body exerts on mass. Thus, an astronaut on the moon has the same mass as on earth but weighs far less, about onesixth as much as he does on earth.

Do we have to take children to the moon to demonstrate the difference between mass and weight? Film strips of[193] astronauts walking on the moon would serve. There is also recourse to the child's common experience. An object placed in water is buoyed up by a force equal to the weight of the displaced water. This fact is known as Archimedes' principle. Thus, a swimmer is buoyed up by the weight of the water he displaces, which is just about his weight, and so he is weightless in the water. If a spring whose upper end is held fixed is placed so that the bottom just reaches and is attached to the swimmer, his mass will not extend the spring.

If an object is heavier (in air) than the weight of the water it displaces, it will sink. Water weighs 62.5 lbs. per cubic foot. Given the weight in air and the volume of a piece of lead or other substances, one can readily frame arithmetic problems that ask whether the objects will float or sink in water.

Archimedes' principle applies also to objects in the air and accounts for objects rising instead of sinking. Helium is lighter than air. If a balloon is filled with helium, its weight is less than the weight of the air it displaces. Hence, it is forced upward by the weight of this displaced volume of air, and since its own weight, which pulls it downward, is less, the balloon rises. It is easy here, too, to raise simple arithmetical problems on the motion of the balloon.

A good case can be made for including in elementary school the elements of statistics and probability. The citizen of the United States is faced with statistics in practically every broadcast and in the daily newspapers. The most important decisions of life, as Laplace pointed out almost two hundred years ago, are made on the basis of probability. Even trivial ones, such as the decision to cross the street, are made on the same basis. The interpretation of statistics is by no means simple and the significance of a probability of, say, 0.75 depends very much on whether it applies to a horse race or a medical treatment. Of course, political leaders and others with axes to grind use statistics and probability to[194] mislead people. Hence, some knowledge of these subjects and their applications to daily life is important to all citizens.

Commercial problems are relevant. Certainly, compound interest should be understood by every citizen, as should the subject of discount. Young children may not be excited by such topics, but perhaps challenging questions would help. If a storekeeper reduces the price of an item by 10 percent and then increases the price by 10 percent, has he restored the original price? Which is the better buy: an item subject first to a discount of 20 percent and then to a discount of 10 percent of the reduced price or the same item subject to a discount of 10 percent and then to a discount of 20 percent of the reduced price?

The elements of geometry are now introduced in elementary school. This is useful knowledge. But as currently taught it seems to be innovation for the sake of innovation. Children are asked to learn any number of terms - acute angle, right angle, obtuse angle, straight angle, and dozens of others - and to know what they mean pictorially. But nothing is done with this knowledge to give it purpose in the eyes of the children. Fortunately, there are dozens of interesting and simple applications.

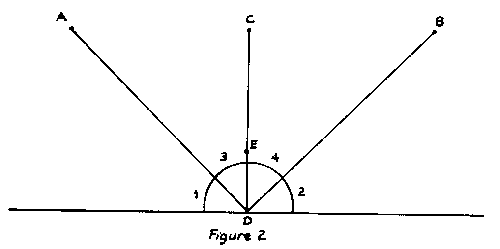
It would be helpful to see some uses of angles beyond their being parts of triangles. One of the commonest [195] applications is to mirrors. A mirror reflects light in accordance with a very simple principle, called the law of reflection.

This law can be readily demonstrated in a classroom by darkening the room, laying a small mirror flat on the desk, and using a pencil flashlight to show the incident and reflected rays. Since every child uses a mirror, the law should be of interest.

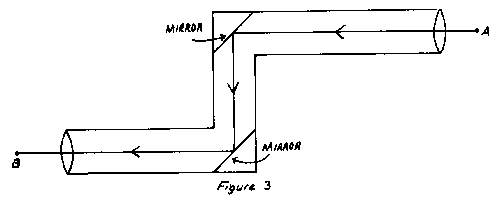
To further impress the student with the importance of angles one can describe or even demonstrate the use of the law of reflection in a periscope. A ray emanating from A (Figure 3) is reflected twice and reaches B.

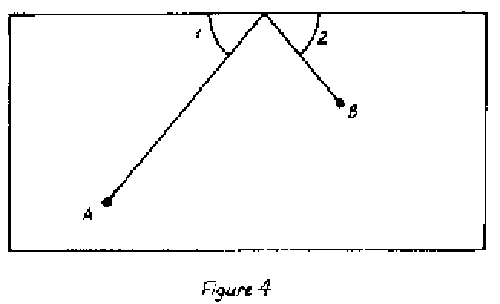
The law of reflection also applies to billiard balls. If a ball [196] at A (Figure 4)is to hit the ball at B by being bounced off the side of the table, the ball must be directed so that

Elementary geometry can be applied to astronomy, preferably with the aid of a model of the solar system, which is commercially available. In this model the sun, the planets, and their moons revolve in precisely the orbits they follow in space and with the correct relative speeds. Such a model is worth far more than any verbal description, diagrams on the blackboard, or pictures in books. A number of mathematical themes - the velocities of the planets, the varying length of the day throughout the year, and eclipses - can be treated readily with the aid of this model. One might object that the subject belongs to astronomy. It belongs to knowledge, and mathematics is essentially involved.

Still another area to which the elements of geometry can be applied is geography. Latitude and longitude are angles formed at the center of the earth. Students can compute distances traveled along a meridian under a change of, say, 5 degrees of latitude or distances traveled along the equator or a circle of latitude under a change of 5 degrees of longitude. (In some instances information such as the radius of a circle of latitude would have to be supplied.) Some applications are mundane but practical. Students might be asked to consider the areas of various rectangles [197] with the same perimeter. Thus, if the perimeter were 100 feet, the dimensions could be 1 by 49, 2 by 48,4 by 46, 10 by 40, etc. By using arithmetic and the formula for the area of a rectangle, students would soon discover that the maximum area is given by a square with dimensions 25 by 25. This result is useful. If a farmer wishes to use only 100 feet of fencing, he can have more area for planting if he chooses a square. Or consider a fifty-story office building. The cost is determined mainly by the walls, but the income is determined mainly by the number of square feet of space that can be rented. Thus, the square shape pays off on each floor. Of course other factors, such as the shape of the land, may not allow the use of the square shape, but the closer one comes to it the more floor space will be obtained. Later, on the high school level, the proof that the square furnishes maximum area can be taken up.

[198] Thus, the roadway is only 27 feet longer than the circumference of the earth -exactly as much longer as the circumference of the fence is longer than the circumference of the garden.

The introduction of scientific applications of mathematics is a lesser problem to the elementary school teacher than to the secondary school teacher. The elementary schools now teach some science, and since the same teacher teaches all the subjects, he or she knows the science involved. Why not teach what is relevant to mathematics in connection with mathematics? The rigid segregation of subjects, which calls for teaching arithmetic at ten o'clock and geography at eleven, is artificial and works against the major goal of education: the integration of all knowledge.

The above examples of real situations - which provide motivation and application as well as the context in which elementary mathematics can be taught - may convince children that the subject, properly approached, is fascinating. As long as the child can think in physical or sensory terms he is at home. Symbols and words acquire meaning only in terms of sense perceptions. Fortunately, teachers and texts at the level of elementary education are becoming committed to the principle that understanding is intuitive rather than logical and are employing intuitive aids such as children's experiences out of school, activities in the classroom, pictures, measurement, and geometrical schemes to answer the question of why we do things the way we do. Conviction derived from seeing that the arithmetical processes do yield what is physically true, rather than proof in the mathematical sense, should be and is becoming the basis for children's acceptance of the processes.

Laboratory materials are now used extensively as aids to pedagogy. The teacher no longer needs to bring apples to [199] school. In the first two or three grades a teacher now has available any number of devices, including Cuisenaire rods, cards, discs, balances, scales, fraction bars, geoboards, clocks, tapes, various types of rulers to perform measurements, geometric models, spinners (to teach probability), and blocks of various sizes, colors, and shapes to represent units, tens, and so on.

Games and puzzles motivate at the lowest elementary school level and it is pleasant to note that these, too, are currently being introduced. For very young children Plato gave this advice over two thousand years ago in The Republic: "Do not, then, my friend, keep children to their studies by compulsion but by play." Many commercial organizations are now manufacturing games, and school systems are buying them.

Sadly needed are laboratory materials for the higher grades. One of these, the hand calculator, is coming to the fore and will undoubtedly aid in the learning of arithmetic. (Its precise value will be discussed later.) Laboratory materials, introduced only in very recent years, were advocated by great educators centuries ago. Montaigne and Rousseau advised us to teach the very young with the aid of real things - let children learn by doing.

Through building up elementary mathematics on the basis of physical problems, real phenomena, and laboratory materials, we seek, of course, to teach understanding of the skills in the hope that the understanding will help in remembering the skills and aid in determining where to use them. However, full understanding of our present-day arithmetic is not easily attained, even with the best of pedagogy, because our system of arithmetic is sophisticated - at least for youngsters. Yet the skills should be acquired early in life. The resolution of this difficulty is not to abandon the teaching of understanding but to [200] emphasize the acquisition of the skills. Though the child's understanding may not be complete, or even though he may forget the justifications of the operations, much has been gained by the presentation. Receiving it at least once has a psychological value. It sets the mind at ease, whereas in the absence of understanding the mind remains perplexed and balks at performing. The situation is somewhat the same as when an adult is called upon to donate money to charity. He wants to know why this charity and not some other. Having satisfied himself, he gives freely rather than grudgingly; and in future years he gives without questioning because he remembers not why he chose this particular charity but merely that he had satisfied himself that it was worthwhile. So it is with skills. Having understood why and having learned how to perform them, in the future one performs them without hesitation. One need not and, in fact, should not rethink through the why. As Alfred North Whitehead points out:

It is a profoundly erroneous truism, repeated by all copybooks, and by eminent people when they are making speeches, that we should cultivate the habit of thinking of what we are doing. The precise opposite is the case. Civilization advances by extending the number of important operations which we can perform without thinking about them. Operations of thought are like cavalry charges in a battle - they are strictly limited in number, they require fresh horses and must only be made at decisive moments.

There are professors who still believe that we can give priority to the concepts and thereby impart understanding. Then, supposedly without much drill, the acquisition of technique will be achieved. Today some go further and argue that the teaching of arithmetic skills can be dispensed [201] with entirely. Students and adults will use hand calculators. As is often the case with new devices, their value is exaggerated beyond all reason. They become the new fad and the excuse for countless worthless papers and talks.

The prospect of hand calculators replacing arithmetic skill conjures up rather ridiculous scenes. Apparently men and women will carry calculators to shop in stores, to decide how much of a tip to leave to waiters and to cab drivers, and to decide how many nickels, dimes, and quarters one needs to pay a subway fare. Perhaps if we were training people only to operate modern cash registers in our grocery stores, the reliance upon calculators would do.

Peculiarly, many of the very same people who favor a curriculum that will prepare students for college mathematics are the ones who would dispense with teaching skills and would substitute the calculator. But students who will go to college must go to high school. And there they will be asked to perform calculations such as 1/a + 1/b, a^5.a³, and (a + b^)2. The best rationale one can give to students of algebra is that letters stand for numbers, and if one knows how to perform the corresponding operations for numbers, the operations with letters are readily justified and performed. The addition 1/a + 1/b is carried out in precisely the same manner as 1/2 + 1/3. Hence, one must learn the skills of arithmetic to do algebra.

Moreover, even after pushing buttons to perform an arithmetic operation, one should check to see that the answer is reasonable. One might have pushed the wrong button. But estimation as to the reasonableness of an answer calls for knowing a good many arithmetic skills.

The hand calculator can be compared with the typewriter. One can use the latter and dispense with handwriting, but the typewriter does not tell us what to say and how to say it. Similarly, the calculator will not tell us what operations to[202] perform or whether the answer is reasonable. Its value is limited. To one who knows arithmetic and how to use it, the calculator can serve to speed up long series of calculations or calculations with large numbers; it is useful as a check on calculations performed with pencil and paper and thereby serves as a teaching aid; and it does provide a gadget that youngsters can finger and so introduces some novelty. But it cannot replace the teaching of arithmetic skills.

The training of prospective elementary school teachers should, of course, include an understanding of the physical phenomena that may be used to motivate students and to apply arithmetic and geometry, and it should include the use of resources such as laboratory materials. College courses for prospective teachers should also foster many more pedagogical aids, some of which can merely be mentioned here.

Terminology should be and some of it, fortunately, is being improved. In earlier times, when students were taught how to perform the subtraction problem 24-19 they were told to borrow 1 from the 2 and to place it alongside the 4 to make 14. They could then proceed. The term borrow was a poor one. One might as well have chosen beg or steal. And borrowing, as Polonius said to Laertes, "dulls the edge of husbandry." Moreover, if one borrows, then one should repay. But there is no repayment. The better term is exchange. (Regrouping is also used.) One takes one of the two tens, converts or exchanges it for ten ones and adds these ten ones to the four. One has exchanged one ten for ten ones, just as one exchanges a dime for ten pennies.

False application of techniques can be a challenging call for critical thinking. Students are taught, rightly, that division of one whole number by another is repeated subtraction. Hence, 7 divided into 28 might be carried out as [203] follows: One tries 1 as a trial quotient and subtracts. This gives:

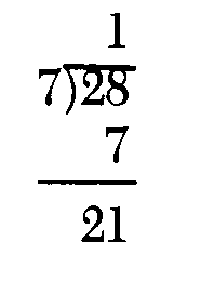
But now 3 can be the next trial quotient and, in fact, 7 divides evenly three times into 21. The false procedure then is to write:

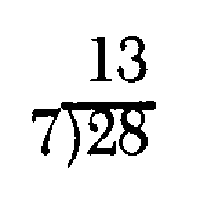
and the answer is presumably 13. Though the flaw may seem trivially obvious to an adult, it is not so to the child. Of course, there are many subtler false arguments and processes that can be employed to advantage.

At some stage in the primary school curriculum students should become fully aware that numbers are abstractions. Simple situations can be used to make the point. A man goes into a shoe store and buys three pairs of shoes at $20 a pair. The salesman says that 3 pairs of shoes at $20 a pair cost $60, and he expects the customer to hand him $60. But the customer instead replies that 3 pairs of shoes at $20 a pair is not $60, but 60 pairs of shoes, and he asks the salesman for the 60 pairs. Is the customer right? As right as the salesman. If pairs of shoes times dollars can yield dollars, then why cannot the same product yield pairs of shoes? (The physicist would give a dimensional argument, but this is a crutch.) The answer is, of course, that we do not multiply shoes by dollars. We abstract the numbers 3 and 20 from the physical situation, multiply to obtain 60, and then interpret the result [204] to suit the physical situation. In this example the clerk's physical interpretation is the correct one, at least in our economy.

The injunction to teach discovery has by now become hackneyed. The fact that it is difficult to do undoubtedly explains why it is rarely done. One must prepare a series of leading questions for each topic and, often without seeming to do so, reformulate a student's reply so that it leads to a useful suggestion. The process is also time-consuming, and many teachers complain that they can't cover all the ground of the course if they teach discovery. But covering ground that succeeds only in causing dislike and even failure certainly accomplishes little. It is not possible here to present the discovery approach to the many topics that have to be taught in the elementary school. But a simple numerical example may serve to illustrate the idea. Students can be presented with the following facts:

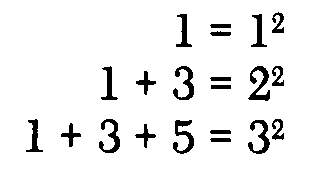
They can then be asked to generalize. They need not write the generalization in symbolic form, but they might be able to state in effect that the sum of the first n odd numbers is the square of n.

This conclusion can be supported by interesting diagrams that, in fact, were first used by the Pythagoreans of the sixth century B.C. (Figure 5).

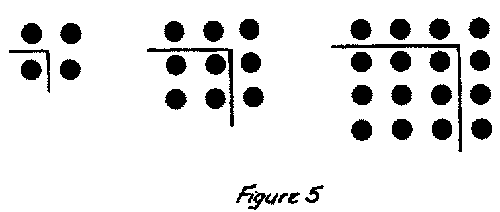
One sees in these diagrams how the addition of an odd number of dots, those above and to the right of the solid lines, produces the next square number. Further, granted the conclusion, the student can be asked to state, without adding, what the sum of

1 + 3 + 5 +...+ 97 + 99

is. There are many such examples, involving only simple properties of whole numbers, that can reasonably call for discovery. The application described earlier of finding the rectangle of maximum area with given perimeter can be posed as a problem calling for discovery of the fact that of all rectangles with the same perimeter, the square has the most area.

Though education in arithmetic has made some progress since the 1970s began, there are still dragons roaming the land, and these must be slain if further progress is to be made. College professors attach very little importance to the courses addressed to prospective elementary school teachers. But these courses are as important as any that professors teach. How these elementary school teachers perform later is crucial. Children start to learn mathematics from the moment they enter school. Their success or lack of success will affect their attitude toward the subject, their confidence in themselves, and, very likely, their attitude toward all [206] learning. Poor mathematics education may be the rotten apple in a barrel of sound ones and by contamination spoil the rest. It is in the course of their elementary school work that far too many people decide that they do not have mathematical minds. Actually, they are victims of teachers who have themselves been victimized by college professors. People "do not have mathematical minds" because they do not receive decent mathematical teaching. Meaningless mathematics will not penetrate any minds. And one who is frustrated by arithmetic will retain an inferiority complex toward all of mathematics, because the subject is cumulative. Even where arithmetic is not a prerequisite, as in large areas of geometry, the mere fact that these are also part of mathematics causes students who have been burned by arithmetic to refuse to let their minds be kindled by new themes.

Mathematicians do like to foster the impression that there is such a thing as a mathematical mind that eo ipso is necessarily superior. Though the existence of such minds is highly unlikely, there is the probability that creativity of the Einsteinian caliber does require exceptional abilities. But it is certain that one does not have to have a mathematical mind to understand mathematics.

The courses that colleges offer to prospective elementary school teachers are usually a waste of time. Typically, they teach the very same topics that the current so-called liberal arts course offers - the logical development of the real number system; set theory; transfinite numbers; Boolean algebra; truth tables; abstract mathematical structures such as groups, rings, and fields; finite geometries; and a heavy emphasis on axiomatics and proof. In fact, the very same texts that are written for the freshman liberal arts course are advertised and used for the courses addressed to prospective elementary school teachers. Even in the heyday of the New [207] Math these topics were inappropriate. Elementary school teachers do not need to know this material and even get wrong ideas from it concerning what mathematics is about and how mathematics should be taught.

Despite the shattering effects of past and current education of elementary school teachers, there is reason to be optimistic. Dragons, especially the mythical ones, have been slain in the past. The current educational dragons, even though devoutly believed in by professors, are also myths; these, too, can be slain.

I am very grateful for the kind permission of Professor Kline's widow, Mrs Helen Kline for this book to be reproduced.

Version: 21st December 2018

Back

[HomePage] Prof Morris Kline