| [HomePage] | Prof W.W.Sawyer | |
NOTES ON THE ART OF PASSING EXAMS.
W.W. Sawyer.
Tactics on the eve of an examination.
Some years ago I heard of a boarding school that was a perfect example of what not to do when an exam is imminent. Before the geometry exam (which in those days dealt with a version of Euclid) the boys spent a large part of the night in the lavatories trying to mug up a number of propositions. This was entirely wrong on two counts. One effect of it was to leave them physically exhausted and thus with no mental energy to cope with the exam. The other effect was to damage whatever knowledge of the subject they had succeeded in building up in the previous months. It was as if their previous knowledge formed some sort of picture of the subject, and the last minute brought a variety of objects in front of that picture, obscuring some of the picture and giving undue prominence to the last minute fragments.
My own practice when I was a student was to cease work on the subject several days before the examination, so the information could settle down in my mind, and take plenty of exercise so as to be in excellent physical condition when the day of the exam came. Incidentally, this reference to physical fitness reminds me of the myth of the "pale scholar", which is completely without foundation. The outstanding workers in many fields had the physique of Olympic athletes. Someone who had made a study of genius wrote that if you collected geniuses together you would have a zoo of splendid animals.
Tactics during an examination.
Success in an exam can depend very much on the procedure you follow during the acual examination. Some students begin (which seems very reasonable) by picking out the questions they are confident about and answering them immediately. However this is not the best procedure. A better method, which in the past was usually recommended to students, was to start by reading all the questions sufficiently carefully to make sure you have understood what they are asking. Only after you have done this should you answer the questions you find easy. The reason for doing this is to take advantageof the the way the mind works.
You have probably had the experience of trying to remember something you are sure you know - someone's name perhaps - but it will not come. You give up and go on to thinking about something else. Then suddenly the namepops up into your mind.
In the brain only a minority of cells are dealing with the thoughts we have at any time. There are others carrying on activities which they do not bother to report. In the case of a name we ought to know but cannot recall, part of the cells will be searching for the records of the name we want; when they find it, they send it up into your consciousness.
It is very helpful to make full use of this power of the brain, the ability to work on a problem when you are not thinking about it. A very successful chief engineer at Liverpool docks told me how he organized his time. There might be some problem that he felt he would need to think about for two hours in the coming week. He would allocate four periods of half-an-hour to this problem. He always found at the beginning of an interval he was further ahead with it than he had been at the end of the previous interval. While he had been thinking about other things, some part of this brain had continued to sort out the issues connected wih the problem.
It is quite likely that this kind of process will be happening while you answering the easy questions. You may well find an idea comes into your mind that fills the gap in the answer to one of the questions you were uncertain about.
If you had not followed the recommended procedure, that idea might have come to you, but perhaps
too late, after the exam was over. The early reading of the question stirs things up in your mind, and increases
the chance that recollection will come before the end of the exam. The delayed action of the mind was recognized
im the French phrase "the wit of the staircase".
This consists of all the clever things you might have said during a party, but you only think of them too late,
after you
have left.
[Note from Mark Alder. I actually developed and used this technique myself many years ago. When taking an examination, I would obtain a spare piece of blank paper and whilst writing down the answers to the easy questions, would jot down little bits of the answers to the difficult questions as they would "pop up" into my mind. It is interesting that this latter kind of information would not "emerge" into my consciousness fully complete and organized. The structure or organization would only become available at the end of the process or when I decided to give the difficult question my full attention.]
Strategy in the months before the examination.
The strategy required will obviously depend on the situation, whether the object is to secure a bare pass or to demonstrate great brilliance.
A friend of mine asked for my advice on GCSE; he was teaching a class with very poor mathematical background,so he would be delighted if anyone secured a pass. He sent me a page of a practice exam. I noticed that 29% could be earned from questions on arithmetic and 16% from questions on algebra, with a total of 45% which should be sufficient for a pass. I suggested his plan should be for the students to make absolutely certain of full marks on these questions, and then to pick up whatever they could manage on the other topics.
In some examinations it is known that certain formulas will be used and these may be printed in the exam paper. However is very unwise to apply these in your work by blind rote and rely on finding them in the actual examination. It is necessary to understand what a formula means and how to apply it. Often it is possible to work it out for yourself and this is the ideal way to master it and understand it. For example, suppose you need to know the equation of a line that starts at height c when x = 0 and rises by m each time x increases by 1. This situation is shown in Fig 1 below.
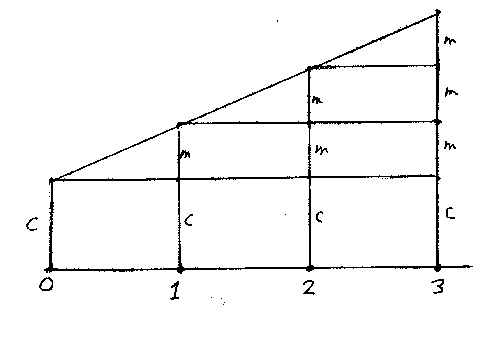
Fig 1
Looking at this diagram we can see that we have the table-:
|
x |
0 |
1 |
2 |
3 |
|
y |
c |
c+m |
c+2m |
c+3m |
which suggests that the equation is y = c + mx. It does not matter that this is not a strict logical proof; we have not looked at what happens between
the whole numbers, if, for instance, x is 2.73
or ![]() . All that matters is
that it is an argument you could have used if you had been the original discoverer of this result; it seems reasonable
and it enables you to see what is happening.
. All that matters is
that it is an argument you could have used if you had been the original discoverer of this result; it seems reasonable
and it enables you to see what is happening.
Beginners at algebra may find difficulty reasoning with the letters c and m, and may need to start with particular numbers and work towards the symbolic general statement. The work above is not only a way of understanding this particular formula; it is helping towards understanding the nature and purpose of algebra.
It is good to go through the above argument every time the equation of a line is being used. It will be found that part way through the thinking, the final answer will flash into the mind. With further repetition this will happen earlier and earlier, until a stage is reached when the formula, its meaning and the picture it represents will simultaneously spring into the mind, a very satisfactory state of affairs.
Check List.
It has been shown the one is more likely to remember an event that happened several years ago, if one has thought about it from time to time, even very briefly, in the interval. The same principle applies in preparing for an examination; it is desirable to refresh your memory of each topic fairly frequently.
What is needed is rather less than a summary of the information in the course. It is more like a check list, that you can look through from time to time and remind yourself of the various things you are supposed to know. It need not contain words. For instance, a little sketch of Figure 1 should be enough to remind you that you are supposed to know the equation of a straight line, and that it would be good to go again through the method of thinking it out. If there is some topic you have tried to understand, but have not been able to do so, leave it out of your list. There is no point in reminding yourself of what you do not know. Going through the list from time to time will ensure that you continue to possess knowledge of the topics where your efforts succeeded.
Copyright © W. W. Sawyer & Mark Alder 2000
Version: 26th November 2020
|