| [HomePage] | Prof W.W.Sawyer | |
PROBLEMS IN THE TEACHING OF MATHEMATICS
Lecture given to the Indian Mathematical Society approximately in 1946.
W. W. Sawyer,
Mathematical Department,
College of Technology,
Leicester.
England
Probably there is no subject which offers such possibilities for misunderstanding between teacher and pupil as mathematics does. The teacher stands at the blackboard. It is perfectly clear to him what the symbols mean, and what the conclusion can be drawn from them.. It is completely otherwise with many of the pupils. What the symbols are meant to represent, how the teacher knows what is right and what is wrong, what is the object of the whole business anyway - all this is wrapped in mystery. The great majority of students say to themselves, "We shall never learn this stuff, but we want to get through the exam. We'll have to learn it by heart."
This is not a satisfactory state of affairs. This learning by heart not only imposes a quite unnecessary strain on the student; it is also quite useless. It gives neither an understanding of the subject, nor the power to apply mathematics in ordinary life.
The more we can see things from the pupil's point of view, the better teachers we shall be.And the first question in the pupil's mind is, "Why do we have to do this at all?" When I was at school, the boys were always asking this - and they never got a satisfactory answer. The teachers made up all kinds of answers, but they were none of them very convincing. The fact is, I think, that mathematics is taught because it is the custom to teach it.
Now a custom may be a good custom or a bad custom, or, more often, partly good and partly bad. It often helps in judging a custom lf we know its history, how it began and how it developed; and I should like to consider the history of mathematics.
Man has, been on the earth for something like half a million years. Mathematics is not nearly so old - at the outside perhaps 20,000 years. Our early ancestors had no schools, no mathematics. What led. them to depart from that happy state? Still more, how were they able to get away from it? How was it possible for them, without textbooks and without teachers, to discover mathematical truths for themselves?
It seems fairly clear that mathematics first arose in purely practical questions; arithmetic in connection with trade, the gathering of taxes, the reckoning of the calendar, etc: geometry in connection with building and land-surveying.
There are two points to note in these early developments: first, there was a c1ear and definite purpose in the minds of the men concerned: second, they were thoroughly familiar with the materials concerned. I do not believe there can be satisfactory reasoning unless these two conditions are satisfied - and in many schoolrooms to-day they are not satisfied.
One marked feature of these practical problems is that they are self-checking. If a man was trying to build a house, and he found that his bricks would not fit together and there were holes for the wind to blow through - he know that he had not solved his problem. (I have in mind that students often do not know whether they have solved a problem or not. They ask, "Is this the answer? Is this what in wanted?")
An interesting example of such a problem is that of finding the length of the year. This problem was solved by a series of approximations, over a period of hundreds, or even thousands, of years. The early guesses were inaccurate, and the consequence of using incorrect values was that months gradually moved from their correct position until July was in the middle of the winter and December in the middle of the summer. The question was, of course, of practical importance in order that the seed might be sown at the correct season.
I believe that children, at any rate when beginning to learn, should follow something of the same path. They should not begin by learning arithmetic for arithmetic's sake. They should set out to do or make some real thing: they should be not sitting at desks, but moving about handling actual objects: and they should be able to judge for themselves whether they or not they have achieved their goal. This stage is all-important. The early years are decisive. If a child does not learn to feel the actual meaning of a wall containing 300 bricks, of a stick being 6 3/8 inches long, of a sack of sand weighing 50 pounds, it will always feel mystified by more advanced mathematics.
I may mention two examples in arithmetic, which I have sometimes found useful. One is the making of models to scale. Boys in England are interested in aircraft; so they make or draw aeroplanes to scale. If they make a mistake, they soon recognize the fact, and seek it out for themselves. Accuracy is even more necessary if they want to understand some complicated machine - for instance, the sliding valve gear on a locomotive. If the parts are not made properly to scale, the apparatus will not properly demonstrate the effect it was intended to.
The second example is deciphering simple codes. The . letter which occurs most frequent1y in English is "e". Hence the symbol which occurs most often is likely to stand for "e". And so on for the other most frequent letters. (see Edgar Allen Poe, The Gold Bug for further details.)
These examples I mention because (from the child's point of view) there is some purpose in them. Indian boys and girls may have special interests of their own. The principle is the same; we should ask, "What do they want to do? Can it be done without calculation?
The most pointless subject, judging by the textbook examples, is algebra. A man buys various articles; then he forgets what he paid for them, and has to work out the prices by simultaneous equations. Does anything remotely like this ever happen in real life? It so, does it occur often enough to justify wasting the precious hours of one's youth on it?
A1gebra is in fact a most important instrument of modern life, though not in such applications as that just mentioned. It is a subject which we in Europe owe to Indian mathematicians
The main problem (it seems to me) which led to algebra was the making of trigonometrical tables, which in turn arose from the needs of astronomy and (more particularly in Europe) from navigation. The interest in tables of square roots and the solving of cubic equations derives mainly from the equations such as-:
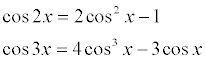
Such equations were. used to find the sines .and cosines of angles in the well-known way, starting from 90o , 45o , or 30o, and then bisecting or trisecting the angles.
There was of course a good deal of work required to calculate the tables, and any way of shortening the work was welcome. Anyone who works or a long time computing tables is bound to notice certain properties.. There is the famous identity discovered in this way-:
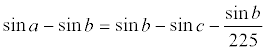
In which c, b, and a are angles which follow each other in a table with intervals 3o45'. This identity was used by mathematicians in India to lessen the work of computation.
Just as geometrical discoveries are easily made by one who is familiar with the shapes of things, algebraic results are easily discovered by one familiar with the handling of figures.
Suppose, for instance, one had to make a table ot reciprocals. One starts off working by long division - a fairly laborious process. One obtains the results the results-:
|
Number |
Reciprocal |
|
1.000 |
1.000 |
|
1.001 |
0.999 |
|
1.002 |
0.998 |
|
1.003 |
0.997 |
But here a property leaps to the eye; as the number rises by .001, the reciprocal falls by .001. This is a far simpler way of getting the next few results than long division would be ,provided (and this is where algebra comes in) one can find out how long this rule can be trusted to give the correct result.
This point should be stressed in teaching mathematics - that algebra was developed with the object of avoiding long long arithmetical calculations.
This is an object which most children will sympathise.
There were very many results similar to this one discovered by the early computers of logarithmic tables. The "table of difference" at the side of the log. and trig. tables is a case in point.
Children should be given a chance to find such rules for themselves and be encouraged to find labour-saving devices in their work, so that they gradually discover algebra for themselves.
It cannot be too much emphasized that each mathematical subject grew gradually out of the previously known subjects.
Algebraic symbolism in particular developed gradually. Far too many algebra books spring suddenly into full symbolism, which is quite unintelligible to learners.
The process by which symbolism arose is very natural and easily understood by children. When children are writing notes on history, they get tired of writing some long phrase such as "William the Conquerer". and they shorten it to something like "W. the Conk" or "W.T.C.".
And that is all that Algebra is. The first general statements about arithmetic were written out in grammatical language (in verse, even) then in the Bakhshali Manuscript "phalam" (equals) is abbreviated to "pha" and "yuta" (addition) to "yu". Bit by bit this process of abbreviations was continued until it reached our present form of symbols.
An interesting phase of this process is Brahmaupta's practice of indicating numbers by colours. He would have given the formula for the rectangle something like this -
"Measure the height of the rectangle and write this down in black ink. Measure the length and write it down in red ink. Multiply the black number by the red number. This gives the area."
This idea might be useful in teaching children today.
While algebraic development was stimulated by the need for trigonometrical tables, this particular application is less important to-day. We have the tables all calculated and finished, and do not need to calculate them for ourselves. In any case, we should use series and interpolation by finite differences, not cubic equations, if we had to recalculate the tables.
The most widespread elementary use of Algebra in the modern world is the application of technical formulae. A mathematician reads a formula at a glance. The ordinary student does not. It is important that a fairly long time should be devoted to enabling learners to feel the significance of a formula.

The strength of the beam increases with increased breadth and depth, but the longer the beam is, the less weight it can support. This is reasonable. It should be second nature with students to apply such general checks to formulae. Books often contain misprints, and the effect of a misprint nearly always is to make the formula quite absurd.
Wherever possible, formulae should not merely be worked out and discussed, but actually applied to the design of real apparatus. For instance, the formula for the expansion of a steel bar due to increases of temperature can be used to design a temperature-measuring instrument. This involves various geometrical calculations also, as the expansion is small, and some means has to be found of magnifying it.
Many other experiments are possible, and can even be done inside a classroom on a small scale - for instance, the formula above for the strength of a beam can be tested by putting weights on small pieces of sticks. It is best if this arises naturally in the course of designing something, e.g. a weighing machine, a small bridge across a stream etc. Scientific laws appeal more to boys if they can see what knowledge of these laws enables them to do.
One can find endless examples simply by looking at a good Engineer's Reference Book.
Just as Algebra tends to be sharply divided from arithmetic, calculus is also often present to students as a completely new and different subject. Very few students realize that the typical problems of calculus were attacked and solved before calculus had been invented.
For instance, one may take Mercator's projection of the globe. This is, of course, not a 'projection' in a geometrical sense like central projection or cylindrical projection. It starts from the problem: assuming the meridians to be represented on a map by evenly spaced vertical lines, how must the parallels of latitude be shown on the map if the track of any ship steering a fixed course is to appear as a straight line?
In modern notation, this would be expressed by the equation-:
![]()
Where y is the height on the map at which the co-latitude (latitude measured from one of the
poles) is marked. This we should solve by integration of ![]() .
.
Mercator however working before calculus was known, did the whole work by arithmetic. In modern
language, we should say that he approximated by taking ![]() not as an infinitesimal but as a finite small number, say 0.001, and then
working out the space which should appear on the map between the two lines of latitude
not as an infinitesimal but as a finite small number, say 0.001, and then
working out the space which should appear on the map between the two lines of latitude![]() . It was then noticed that Mercator's table for the position
of lines of latitude was the same as the table for
. It was then noticed that Mercator's table for the position
of lines of latitude was the same as the table for ![]() .
.
One can see how they came to guess this formula, probably looking at the Mercator map. The North
pole does not appear, it has .
The equator has y = 0. The South pole
has
. The co-latitudes
are 0, 90, 180 degrees, so tan of the half-angle gives 0, 1,
and -log brings these where they should be.
Thus this isolated result was known before calculus existed as a systematic subject.
Calculus, like algebra, began as a set of experimentally observed rules which could be used to shorten long arithmetical calculations.
The old fashioned method of presenting calculus beginning with differentiation of X2 by means of 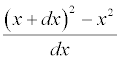 nearly always puts students off.
nearly always puts students off.
They do not feel that it would have occured to them to do this. The procedure based on the historical development, i.e. from a definite problem, through arithmetical approximation, to an empirical law, afterwards verified by algebra, seems to offer less difficulty.
A more detailed study of the practical problems of the 16th and 17th centuries will be found very helpful by anyone who desiures to teach calculus well. These problems covered navigation, map-making, the design of clocks and telescopes, ship construction and mechanics generally.
Some problems of this period, which are not of great interest to-day have become "fossilized" in calculus textbooks. These can be a source of perplexity to students, who ask, "What is the object of this section?"
To be honest with our students, I think we teachers of mathematics ought to go through the mathematics syllabus and classify its contents under the following headings.-
1) Methods of great generality and mathematical importance.
2) Results which are beautiful and interesting in themselves.
3) Methods and results of practical and technical value.
4) Work of historical interest only.
5) Things which we cannot find any reason for including at all.
Lack of space prevents me from developing these ideas as I should like to do but I hope some of them will provoke discussion.
Copyright © W. W. Sawyer & Mark Alder 2000
Version: 26th November 2020