| [HomePage] | |
THERMODYNAMICS.
W. W. Sawyer.
Historical Background.
Sadi Carnot (1796-1832), the founder of thermodynamics, was the son of L.N.M.Carnot, the "organizer of victory" in the French revolution. L.N.M.Carnot was an army engineer. He wrote on mathematics, military tactics and other topics. He played a very prominent part in the politics and wars of revolutionary France. Sadi Carnot was a patriotic Frenchman. He was interested in the application of science to industry. Britain had derived great benefits from its possession of the steam engine, years before other countries. Carnot hoped that scientific understanding of how the engine worked would help France in its rivalry with Britain.
In Britain, the condensing oF steam to raise water from mines had been used as early as 1698. Round about 1770 there were in use steam engines in the modern sense - for producing movement. "Science since 1500" comments that Britain used steam engines for decades and never bothered to study them scientifically. On the other hand theoretical studies were produced in France almost immediately after the arrival of engines there. This of course is typical. Britain, advancing into the unknown, used empiricism, pioneering by trial and error. On the continent, the industrial classes were continually frustrated by working under the control of aristocratic regimes; this indeed was one of the great driving forces of the French Revolution. Unable to do what they wanted, they spent their time dreaming and thinking about the potential of the new developments.
Many useful concepts were already available to Carnot. In 1738 D.Bernouilli had considered gas as a swarm of moving particles, and had shown that an increase in temperature would lead to an increase in pressure. He also had the idea of Conservation of Mechanical Energy (in frictionless processes).
Outline of Carnot's argument.
Carnot raised a fundamental question. He accepted the idea of the conservation of energy, but realized that heat energy, although existing, might be unavailable. (Pledge, Science Since 1500, p.143.) He thought of heat being like water, which drives a watermill by falling from a height (high temperature to low temperature). You cannot get any more mechanical work from the water once it has reached the lowest position available, - similarly for heat. Carnot, like many physicists at that time, accepted the caloric theory, the belief that heat is an enduring substance. Count Rumford, in 1798, from the experience of boring cannon, had come to believe that you could make as much heat as you wanted by performing work. Conversely heat can be destroyed when work is being done. Carnot did not realize "that heat is lost as work is gained".(Pledge, p.143.) This however did not prevent him from arriving at correct and very important conclusions.
It is interesting that we can reach the main point of Carnot's argument without any detailed calculations about the behaviour of gases or other substances. His theorem is this; - no engine can ever be more efficient than a reversible engine.
Suppose the reversible engine works between the temperatures, can produce more work for a given quantity of temperatures T and t. No engine, working between these heat. For suppose the reversible engine can take in H units of heat at temperature T and use it to produce W units of work at temperature t. Being reversible, it could take in W units of work at temperature t and use this to give out H units of work at temperature T. Now suppose some other engine could do better and change H units of heat at temperature T to W' units of work at temperature t, with W' > W. Carnot argued as follows;-
First, let the improved engine change H units of heat at T to W' units of work at t. Use W'-W to do some useful job. This leaves W units, which the reversible engine can change to H units of heat at T. Repeat this process. Each time we get W'-W units of work, and end back where we started. We have perpetual motion which Carnot believed was impossible. Here we have an essential theorem of thermodynamics, freed of technical details.
The Carnot cycle.
The mathematical implications of this theorem are found by considering a particular series of operations, known as "the Carnot cycle", involving the expansion and contraction of gas, with heating and cooling. We suppose the gas to obey the equations for an ideal gas. This might seem to bring in an element of unreality. However the behaviour of actual gases at sufficiently low pressures approximates very closely to that of the hypothetical perfect gas, so that in principle it would be possible to carry out an actual experiment as close as one may wish to a Carnot cycle. All the changes in the volume of the gas are to be carried out extremely slowly. Some of them are to take place at constant temperature, such as might be achieved by having the gas in a metal container in contact with a large mass of water. These are known as isothermal. Others are to be done in such a way that no heat can enter or leave, the container being surrounded by insulation; these are called adiabatic. As the Carnot cycle involves both these processes, we need to calculate the work, heat and pressure changes involved in each of them, before we can consider the Carnot cycle itself.
Adiabatic expansion.
Theory suggests and experiment verifies that the internal energy of a gas depends only on the temperature. For an ideal gas we assume E = CT, where E is the energy and T the absolute temperature.
For adiabatic expansion we have insulation that ensures no heat enters of leaves. The external pressure is lowered gradually, so the gas expands and therefore does work. This work can only come from a reduction in the internal energy of the gas. Thus dE = -p dV. Now dE = C dT, so we have
C dT + p dV = 0. .......................(1)
For a mole of ideal gas we have pV = RT, so CT= (C/R)pV.
Hence
(C/R)(p dV + V dp) + p dV =0.
This gives, on multiplying by R and collecting terms involving dV and dp
p(C+R)dV + CVdp =0
Let (C+R)/C = g ...............................(2)
The equation becomes
g dV/V + dp/p = 0
from which it follows that ln p + g
ln V is constant.
Hence, for an adiabatic change
pVg = constant............................... (3)
Adiabatic changes are reversible; the same equation holds for an adiabatic contraction.
Work in an adiabatic change.
Let pressure and volume change from p1,V1 to p2,V2 adiabatically. Then, during the change
p = Kv-g
where K = p1V1g = p2V2g ............................... (4)
Integrating p dV we find the work done is
[K/(1-g)] .[V21-g - V11-g].
By using equation (4) we can show that this equals (p2V2 - p1V1)/(1-g). From equation (2) we see that 1-g= -R/C . Using the equation pV=RT for the initial and final stages, we eventually reach the simple formula for W, the work done
W = C(T1 - T2) ...............................(5)
In an adiabatic expansion the temperature falls, and, as expected, W will be positive. In a contraction the work will be negative, that is to say, work will have to be done on the gas to make it happen.
It is useful to derive equation (5) by considering the details of what happened during an adiabatic process. It can be derived directly from the principle of conservation of energy. At the start, the internal energy of the gas is E1= C1; at the end it is E2= CT2 ; the work done comes from this decrease of energy.
Work in an isothermal process.
This is a process in which the temperature does not change so T is constant. As pV=RT for a mole of gas, p=RT/V and p dV = (RT).dV/V. Integrating this leads to logarithms and we find
W = RT.ln(V2/V1) ...............................(6)
The energy of the gas, being a function of temperature, does not change, so, in an isothermal
expansion, this work can only have come from that amount of heat being absorbed. If the gas is compressed, V2 <
V1, and the work done by the gas is negative and that amount of heat comes out
of the system.
Graphing the Carnot cycle.
In the Carnot cycle there are two isothermal processes and two adiabatic processes. . In textbooks the cycle is usually shown graphically with co-ordinates p and v. There are some advanrages in taking T and v for the variables, as is sometimes done in connection with other problems. In the usual graph, the curves for the two types of process do not look very different. If we take T as one of the variables, it immediately becomes obvious which processes are isothermal, for in them T is constant and the graph is a level straight line. The equation for an adiabatic process was given in equation (3) as pVg = constant. As pV=RT, p=RT/V and the equation becomes TVg-1 = constant. As g=(C+R)/C, g-1=R/C.
Thus we have TVR/C = constant, and so lnT + (R/C)lnV = constant.
Accordingly if we take x =lnV and y=lnT, adiabatic changes will be shown by a descending straight line with gradient -R/C. The nature of the cycle can be read off fom the diagram, Figure 1.
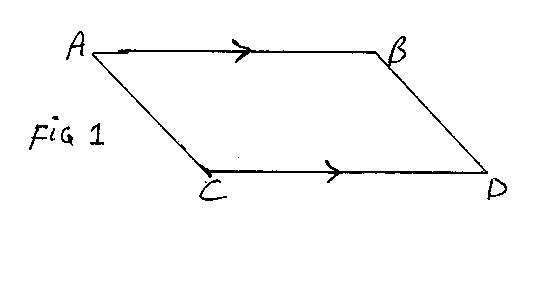
If we begin the cycle with the isothermal change, at temperature T1, from A to B, the lines AC and BD represent adiabatics through A and B respectively. C and D are points on these at temperature T2. In the cycle we go from A to B and then B to D; in both of these the volume increases. We then go from D to C and from C to A; in both of these the volume decreases.
We now consider the total work done and the heat changes in the cycle. As we saw in equation (5), the work done in BD is C(T1-T2), as we go from temperature T1 to T2. In CA we do exactly the opposite; we go from T2 to T1, so the contributions of BD and CA to the work done cancel out.
From equation (6) we see that the work done in AB is RT1(lnV2 -lnV1), where V1 and V2 are the volume at A and the volume at B. Now in the graph we are using, the x-co-ordinate is lnV, so lnV2-lnV1 is simply the length of the line AB. As ABDC is clearly a parallelogram, the length of CD is the same as that of AB. The expression for the work in DC will differ from that for AB only in having T2 instead of T1, and having a minus sign in front, as in DC the gas is being compressed and work is being done against the desire of the pressure. Thus the work done in the whole cycle is
W = R(T1-T2)(lnV2-lnV1).............................. (7)
Now the efficiency of the machine is measured by W/Q, where Q is the amount of heat put into the machine in stage AB. This determines how much coal has to be burnt. Heat comes out of the machine at the lower temperature T2, but this is of no interest to the machine operator. As stage AB is at constant temperature and as internal energy depends only on temperature, the heat absorbed is numerically equal to the work done in AB, which we calculated above. Hence
Q = RT1(lnV2 - lnV1) ..............................(8)
Thus the efficiency
W/Q = (T1 -T2)/T1.............................. (9)
This efficiency is a function of the temperatures alone, and no machine operating between the temperatures T1 and T2 can ever do better.
Copyright © W. W. Sawyer & Mark Alder 2000
Version: 22nd March 2001
|