|
[HomePage] |
Professor W.W. Sawyer | |
Some Thoughts on Examinations
WW Sawyer
Department of Mathematics,
University of Toronto
Recently I heard teachers discussing A-level syllabuses. They were talking very much in terms of small alterations
to the present structure, when a senior H.M.I. said, in effect, "Forget
the present arrangements. The whole system is under review. Consider what you think examinations ought to do and
what regulations would best enable them to do that.'' The present article is written
in that spirit.
The first question is whether there should be any examinations at all. When I worked in Britain I was aware of
various unfortunate effects of examinations. In Ontario I have observed a system where students arc admitted to
university without examination and the consequences are even more unfortunate. It is no kindness to a student to
admit him to a mathematics course for which he is not adequately prepared; he will endure a frustrating, harmful
and purposeless experience. I would therefore like to see a variety of mathematics courses available to students
and adequate testing to ensure that a student gets into a course for which he is suited.
One great defect of examinations in schools and universities throughout the world today is that they lend themselves
to faking. A course is taught in such a way that students do not understand the basic ideas, but they learn to
produce rigmaroles that look sufficiently like mathematics to justify a pass mark. After a few months the rigmaroles
are forgotten; nothing of positive value remains in the mind.
Mathematics involves understanding, techniques amid ingenuity, but without the first of these time other two are
impossible. Unfortunately it is the latter two that examinations tend to stress and it is only by accident that
lack of understanding is isolated and exposed. I heard recently of a student taking a university course in analysis
(!) who answered the question
''How many real roots has time equation ex=x+2 ?" by writing ''It has n roots.''
This answer is totally meaningless and shows that time student does not understand the first
thing about algebra as a language, yet he has collected enought O and A-levels to get into a university course
with mathematics as its main ingredient. Clearly our present examinations do not tell us what we most need to know.
The question now arises, can we devise questions that test understanding rather than routines? I believe this can
be done, and I offer some examples from the beginnings of calculus. It is very unsatisfactory to spend time emphasising
the ideas of calculus and then set a test consisting entirely of "Differentiate 5x2- 3x + 2."
On various occasions I have used a test along time following lines.
Interpret s=f (t) as representing the motion of a car, s miles in t hours. Express by means of s',
s" the following: the velocity of the car (at some instant)
is 60 m.p.h.; the car is stationary; the car is moving forwards, and is accelerating (etc.).
Some graphs are then shown and the pupils have to say what signs dy/dx and d2y/d2x appear to have.
They are asked to sketch graphs in which dy/dx is first positive, then zero, then negative.
With somewhat more advanced students I have used questions such as:-
1) The motion of a car is given by the equation, ![]()
State at what times the car is moving forwards, at what times backwards. Also say at what times
you would expect the driver's foot to be on the accelerator and at what times on the brake.
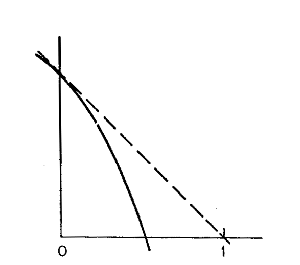
2) Give examples of continuous functions that satisfy the following conditions, or explain why the requirements
are impossible.
(a) f (0) = 1, f (1) =0, f'(x) positive for all x.
(b) f (0) = 1, f' (0) = -1, f"(x) always negative, f(x) =0 having no real solution.
Of course, in each part of this question the requirements are impossible. In (a) the function is required to be
increasing and yet have f(1) less than f(0). In (b) the graph must have the slope and curvature as shown here,
which clearly compels f (x) =0 to have a solution between x=0 and x=l, contrary to the last requirement.
It may well be urged that the supply of such questions is limited, that sooner or later the questions would become
stereotyped and the less intelligent teachers would train their pupils like performing animals to give the expected
answers. Now I have no illusions that, by examination regulations or any other administrative device, bad teachers
can be made into good ones. But we do know that teachers are very much influenced by what they expect examiners
to ask. If it were known that some questions were intended simply to test whether pupils associated the first derivative
with velocity and steepness, the second derivative with acceleration and sense of curvature, even if the teachers
used strange methods of establishing these associations, it would be difficult for them not to give their pupils
at least a chance of understanding the intuitive meaning of calculus.
Examinations at every level might be in sections designed to test basic understanding, technical
competence in straightforward situations, and ingenuity or expertness (this last section being perhaps optional).
The marks for each section would have to be given separately. A mark of (100, 60, 10) might be regarded as very
satisfactory for someone who intended to use mathematics to study, say, economics. A mark of (10, 40, 0) would
suggest that the examinee had mugged up some algorithms with very little idea of what it was all about.
Above I gave examples related to calculus because I had a small stock of these on hand. It should be possible to
devise questions for algebra, not involving manipulation, but testing the ability to talk sense in the language
of algebra. The pupils might be asked to write the algebraic generalisation suggested by a sequence of number coincidences;
such questions allow great variety with finely graded differences of difficulty. The same applies to algebraic
statements arising from some actual situation of problem; e.g., how long is it from x o'clock a.m. to y o'clock p.m.? Since pupils so often
write nonsense of the type (1/x) + (l/y) = l/(x+y), a question might well ask them to classify various equations as certainly true, probably true, probably
false, certainly false. This indeed has practical value. Often in reading some subject you come across a formula
and wonder if it contains a misprint. To derive the formula from first priniciples may be tedious, or may call
for knowledge you do not possess. So you look at the the formula and ask yourself, "Does it behave as it should for large x? Is f(0) what we would expect? Does f(x) increase with x and does this agree with the physical situation?''
A question I once set in a scholarship examination in New Zealand, that was open to pupils of every type, may be
of interest, It ran something like this. ''A scientist wants to find a formula giving the height, h feet, of a male person x years
old. Arrange the four formulas below in order of merit. Can you suggest a formula better than any of them?
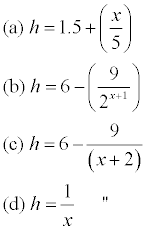
The answers to this question revealed most striking differences in the depth, or shallowness, of the candidates'
thinking.
Somewhere I would like to see questions on the ability to visualise arithmetic in concrete terms and to think out
arithmetical results and processes. My reason is that this ability is the key to successful primary teaching, and
primary teaching is the most important of all teaching. I would like this intuitive insight into arithmetic to
be fostered as early as possible in a future teacher's life; usually, by the time students come to university or
college of education, their attitudes have been fixed and it is too late to make any fundamental change.
So far I have stressed understanding, but this does not imply agreement with the view ''Understanding is all that matters, do not bother about manipulation''.
I am urging rather that manipulation should be based on, and continually checked by, understanding. In most branches
of mathematics we can recognise "straightforward manipulations'' which are both necessary and sufficient to show the power and the uses of the branch. Examinations
should expect, and should give recognition to, competence at this level.
Finally, a warning against rushing from one extreme to the other. All the remarks above have some relation to the
problem of giving due recognition to the pupil who has some basic knowledge and insight into mathematics, without
being able to perform all the tricks of the expert mathematician. To this extent this article ties in with the
School Council's concern for reduced specialisation in sixth forms. But this phrase ''reduced specialisation'' is a dangerous one. I hope it will mean that
a broad programme of studies will be available for those who need it and want it. I hope it will not mean that those boys and girls who discover their central purpose early
in life will be prevented from concentrating their efforts on it. If there are to be five A-levels, I hope no officious
body is going to draft regulations that will forbid any pupil choosing (1) mathematics, (2) more mathematics, (3)
still more mathematics, (4) advanced mathematics, (5) very advanced mathematics, if that is what he or she wants
to do.
The object of an educational system is to assist the development of' every kind of individual. We create simply frustration and rebellion if we bar the path of someone who knows
where he wants to go.
I would like to propose very strongly an Axiom of' lgnorance.
It states: teachers do not know what is best for every pupil. Charles Darwin is a superb example. From boyhood he was interested in collecting butterflies and beetles;
later he spent time talking to pigeon-fanciers. These were excellent preparations for his future work but were
not then regarded as falling within school studies. Darwin was regarded as a failure by his father, by his teachers,
by his professors and apparently by himself. Fortunately in his case the conscious efforts of men were not strong
enough to overcome the unconscious forces of life, but we have no right to assume that these forces will always
heal the ills created by our narrrow-mindedness and petty tyrannies.
Ostwald, who was both a great scientist and a great teacher, wrote interestingly on the evaluation by teachers
of a dedicated pupil. Usually they believed the pupil had shown promise but had then deteriorated. This was because
he concentrated on what he believed inportant, and refused to be distracted by other demands. And this is the key
to success in any large endeavour.
It should not be assumed that a pupil's outlook is narrow because his timetable is concentrated in one area. At
one stage of my time at Highgate School I had what must have been one of the most concentrated timetables in world
history, 24 hours mathematics, 1 hour English a week. But I was also secretary of the Debating Society and an assistant
to the school librarian, which gave me the privilege of borrowing an unlimited number of books. In fact I read
literature of every kind, but I would have hated being forced to do this in a class and then be examined on it.
This is not an isolated experience. For instance, the Russians set up a school for pupils strongly interested in
computer studies. It was found that, as soon as pupils were not forced to read the literary classics, they began
to read these of' their own free will.
We hear many complaints to-day that students are not interested in their subjects, but only in examination marks.
In such a situation it is surely a great pity to discourage the minority who do want to learn some particular thing.
I hope that in reacting against one type of error that has been made in the past we do not commit ourselves to
an equally serious error in the opposite direction.
Reprinted from " Mathematics Teaching, '' No. 69, December, 1974. published by:
The Association of Teachers of Mathematics. email: atm_maths@compuserve.com
We are grateful for the permission of the Association to reproduce the above article.
Copyright © W. W. Sawyer & Mark Alder 2001
This version 20th February 2001
|