| Professor W.W. Sawyer | |
More advanced Mathematics applied to give fundamental Insight.
The Importance of the Unbelievable
Warwick Sawyer
In a lyrical moment Gottfried Leibniz remarked that 'the Divine Spirit found a sublime outlet in that wonder of analysis, that portent of the ideal world, the amphibian between being and not being, which we call the imaginary root of negative unity.' But are 'imaginary' numbers really any more imaginary than 'real' numbers?
The enjoyment of a play or a film is said to depend upon the suspension of disbelief. In the development of mathematics
also there are times when progress depends upon the acceptance of an idea that appears absurd or impossible.
Negative numbers were at one time such an idea. The common sense view reveals itself in sayings such as 'I couldn't care less'. The amount of something
cannot be less than nothing. For many years mathematicians went along with this view. They did not accept a negative
number as a value for a symbol or as the solution of an equation. If asked to solve x + 1 = 0 they would say that
no solution existed.
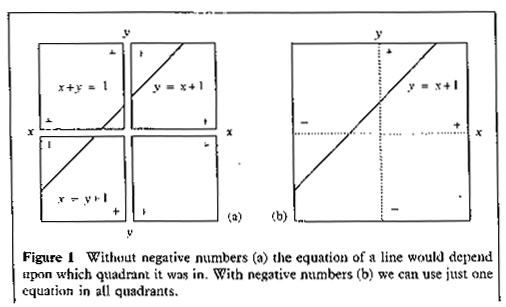
It would be immensely inconvenient if this view had prevailed. In graphical work, for instance, we would need a
different coordinate system for each quadrant of the plane. The equation of a line or curve would change as it
passed from one quadrant to another (Figure 1). If we were seeking a point that satisfied certain conditions, we
would have to try each quadrant in turn until we found one that worked. We would not be able simply to call the
point (x, y) and at the end let the signs tell us where it lay.
Impossible Number?
After negative numbers and the usual rules for calculating with them had been accepted, a new impossibility appeared.
Squares cannot be negative. The equation x2 + 1 = 0 has no solution. But, as the years passed, cracks began to appear in this wall of impossibility.
For example, in the 16th century Italian mathematicians found a formula for solving cubic equations, similar to the usual formula for quadratics, but more complicated. Sometimes this formula gave baffling results. For instance, it was easy to check that x = 4 is a solution of the cubic equation x3 = 15x + 4. But the formula for solving cubics gave
which did not seem to make any sense. In 1572 Raphael Bombelli - after some hesitation
- maintained that the strange formula (1) did in fact yield x = 4. To see why, let us use modern notation, in which
the symbol i is introduced to mean
-1. I am going to assume that you have met the idea of i before, and know how to calculate with complex numbers
and how to represent them as points on the plane; but I want you to put yourself in the position of an ancient
mathematician who has never encountered such an outlandish idea before.
The symbol i cannot denote a number in the usual sense, but we can ignore this problem and explore the implications,
just as even earlier mathematicians accepted that the symbol -1 did not denote a number in what was the usual sense
at the time. What they did for the equation x + 1 = 0, we will do for x2+ 1 = 0. We will assume that the symbol i can be manipulated according to the standard laws
of algebra, together with the rule i2
= -1.
Then (11i)2 = 112i2 = 121(-1) = -121, so \/-121 = 11i.
Thus Bombelli's strange formula (1) becomes
A little experimentation leads to the following calculation:
(2 + i)3 = 23 + 3.22i + 3.2.i2 +
i3
= 8 + 12i - 6 - i
= 2 + 11i
So it is sensible to maintain that
Similarly
Substituting (3) and (4) into (2) we get
x = 2 + 2i + 2 - i = 4
In other words, provided we accept that there is some kind of 'number' i which satisfies i2 = -1, then we can extract the correct answer x = 4 from the formula (1).
An idea that gives wrong answers is clearly nonsense; hut an idea that looks silly but gives correct answers might possibly make some kind of sense if it was looked at in the right way. For more than two centuries after this, faith in the impossible number i -1 gradually grew. Although no one could defend it logically, it kept giving correct results.
The most dramatic advance was made by Roger Cotes in Cambridge in around 1715. He started with the three infinite series for the exponential, sine, and cosine functions:
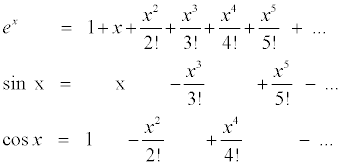
The symbols in the series for ex
can be cut out and placed over the same symbols in the other two series. However, a few minus signs have to he
thrown in. More formally, we can express this as the equation
eix= cos x + i sin x .......... (5)
The ix makes the signs work out properly. What makes this so striking is that it brings together two parts of mathematics
that seem totally separate. We meet sines and cosines in the framework of geometry, involving the lengths and angles
of right-angled triangles. The background of x is entirely different. Expressions involving indices occur in algebra, and the number e is usually
first met in calculus. (See MATHEMATICS REVIEW Vol 1 no. 5) for an article about e.) There is no hint that the
two topics are ever likely to merge.
However, when they do merge it is very welcome. The algebra of powers of e is relatively easy - it depends only on the laws of indices
emen = em+n .......... (6)
(em)n = emn .......... (7)
The formulas for sin(A + B) or cos (A + B) are much more complicated. However, if we accept the existence of that
elusive 'number' i, then we can use (1) to derive trigonometric formulas in a very simple way.
For example, the law of indices (6) tells us that
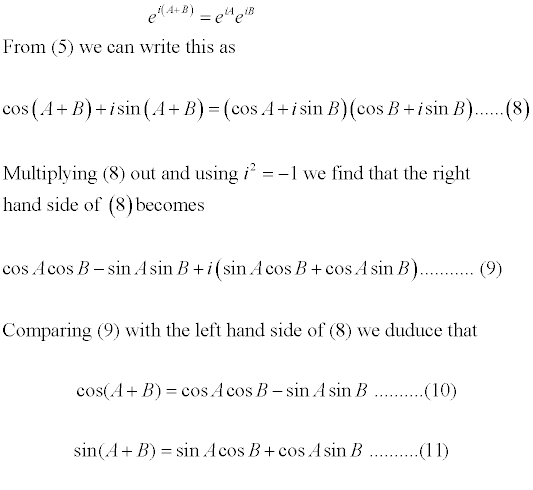
These are two very basic and very useful results which you will have met before. But you probably have not seen them derived using just algebra before. Again this illustrates how useful i is, and that it seems to keep giving correct answers.
Formulas (10) and (11) are similar enough to be confusing. I have found that the best way to memorise a result is to derive it every time I require it. At first this is a slow process, But after I have performed it several times a channel seems to become carved in the brain. Part way through the work, the conclusion flashes into the mind. With repetition this tends to happen more and more quickly.
Some Applications
What we have seen so far certainly suggests that introducing a new kind of number (i) can be useful for mathematics.
But does it have any use in the real world? The same problem arose when mathematicians first invented -1 - its
applications turned out to include temperatures (when a negative value indicates a temperature below freezing),
banking (when a negative value indicates an amount owing), and, as mentioned at the beginning, graphical work (when
different signs yield different quadrants in the plane).
Once we have the 'number' i, we must also have numbers like 2i, 3 - 2i, and so on. Indeed if x and v are any 'real' numbers (including fractions and decimals but not \/- 1) then we must consider x + iy to be a 'number' on the same footing as i itself. We call x + iy a complex number and denote it by z:
z= x+iy
We call x the real part of
z and y the imaginary part of z. The word 'complex' here does not mean that z is complicated; it just means that z is composed of several
parts (namely x and y). Similarly 'real' and 'imaginary' do not have
their usual meanings; they just indicate that 'real' numbers are ordinary numbers whereas 'imaginary' ones are
those that involve the new type of number i. It is not such a bad name - 'imaginary' numbers are a product of the
mathematician's imagintion. (In the modern view, so are 'real' numbers!) You may remember that, just as we can
think of the real number x as lying on a line, we can represent the complex number x + iy by the point (x,y) in
a plane. This is often called the Argand diagram, after the French mathematician, Jean-Robert Argand, who described it in 1806. It was also
invented by a Dane called Caspar Wessel, nine years earlier, and by the German, Carl Friedrich Gauss in 1811. Indeed,
the basic idea is present in the work of the Englishman John Wallis in 1673. To avoid an international incident
we will simply call it the complex plane.
Remember: you do algebra with complex numbers in exactly the same way as with real numbers, but remembering that i2 = -1. For example
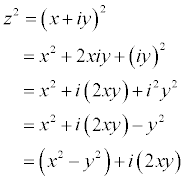
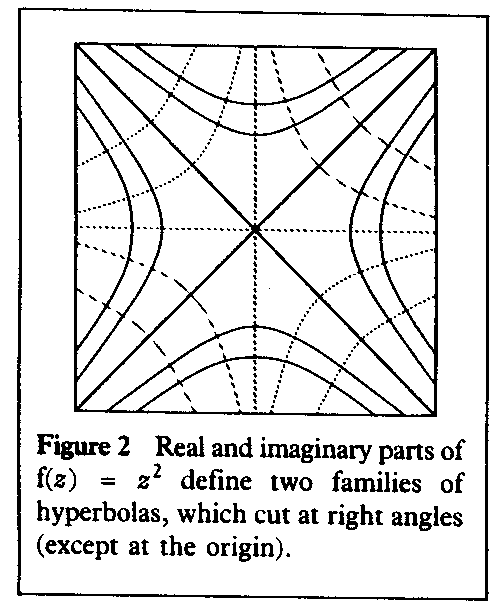
Notice that we started with a function of z, namely f(z) = z2, and we emerged with two functions of x and y, namely the real and imaginary parts x2-y2 and 2xy.
We can use these two functions to define two families of curves:
x2-y2 = c
2xy = k
where c and k are constants. If you sketch these, for various values
of c and k, you will get two families of hyperbolas (Figure 2). Moreover,
all the curves in one family cross all those in the other at right angles.
Amazingly, the same is true if we use any other function of z. For example, with
f(z) = z3 = (x+iy)3 = (x3-3xy2)+ i(3x2y-y3)
we get the families x3-3xy2 = c and 3x2y-y3 = k. With some expenditure of effort you can sketch these families and check the right angle property. A much simpler case is when f(z) = z, and the curves are x = c and y = k. These are just two families of straight lines parallel to the two axes: obviously these cut at right angles (Figure 3).
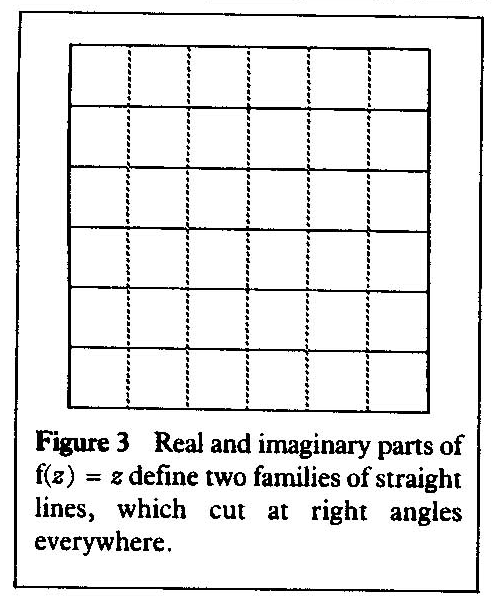
This diagram can be interpreted physically in a variety of ways.
(1) The dotted lines could represent contours of a plane, tilted at an angle to the horizontal. Liquid flows down
the plane at a velocity proportional to the gradient. It moves along paths indicated by the unbroken lines.
(2) A plane is a possible shape for a membrane or soap film stretched on a suitable frame (say a square). The dotted
lines could represent contours specifying this shape.
(3) The unbroken lines could represent electric current flowing through a copper sheet, and the dotted lines the
corresponding equipotentials.
(4) Equally, it might show lines of force and equipotentials in a uniform magnetic field.
Similar physical interpretations are valid for the families associated with any complex function, not just f(z) = z; so there are applications to fluids, soap films, electricity, and magnetism. Nothing 'imaginary'
about those!
Because they are described by the same mathematical idea, these situations have so much in common that we can sometimes
draw on one of them to illuminate another. For instance, the effect of height in relation to gravity can provide
an analogy useful for thinking about electricity or magnetism.
Notice that the physical interpretation of a complex function such as z2, is in terms of two physical properties. That makes sense, because every 'complex' number is assembled from two components; its real and imaginary parts. Naturally any interpretation in the real world will involve two separate quantities. One advantage of the complex notation is that it enables us to consider both quantities simultaneously.
Let us try something a little more ambitious - the function f(z) = l/z. We have to find the real and imaginary parts of l/(x+ iy). There is a nice trick for achieving this, which is to observe that (x + iy)(x - iy) = x2 + y2, which is real. So we multiply numerator and denominator in l/(x + iy) by x - iy, and deduce that
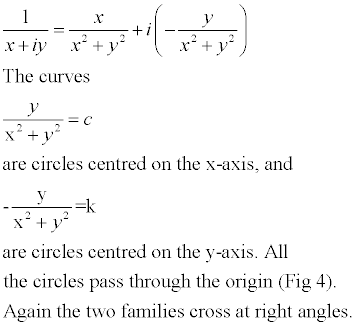
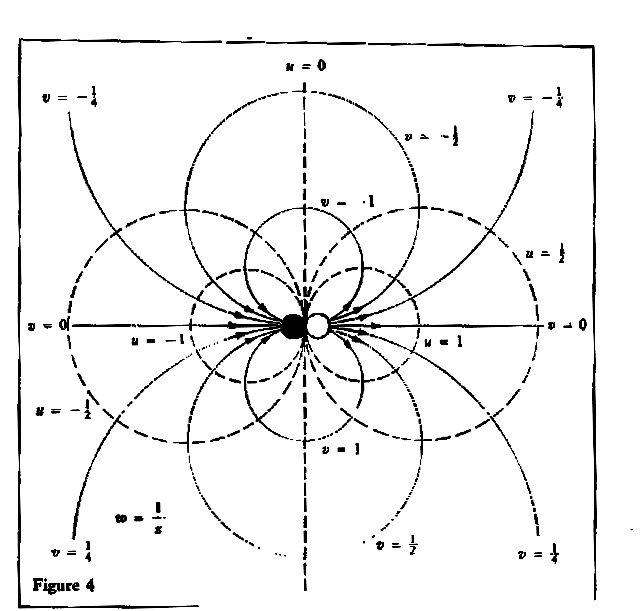
Down the Plughole
We can get an approximate realisation of this pattern as a flow of water if we think of the kitchen sink; the black
circle is the outlet and the white circle a jet of water directed near it. Alternatively, we can imagine a copper
sheet with electric current entering at one point and leaving at another point very close to it.
The diagram also suggests the lines of force of a magnet. Actually, magnetic lines of force are not circles in the real world; but they would be in a two-dimensional world, and this is a very fruitful idea. Figure 4 therefore describes a space that is empty except for a magnet at the origin.
The function l/z from which we started
behaves in a special way at the origin - it becomes infinite. So we conclude that an infinity (or singularity) in a function corresponds to a
point at which an active element, such as a magnet, is placed. Now the active elements determine what happens everywhere.
So a complex function should in some sense be completely determined by its singularities.
We can take the idea that the singularities of a complex function are important and apply it to series. We know
that some degree of care is needed when handling infinite series. For example, summing a geometric progression
leads to the equation
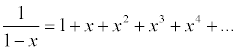
This is perfectly reliable if x
lies between -1 and 1; but if we take, say, x
= 3, then we get the absurd result 
.
It is not very surprising that things go wrong if x goes past the value 1, because 
becomes infinite when x = 1. However, we get no such warning in the case
of the equation
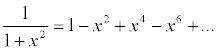
which has the gentle and innocuous graph shown in Figure 5.
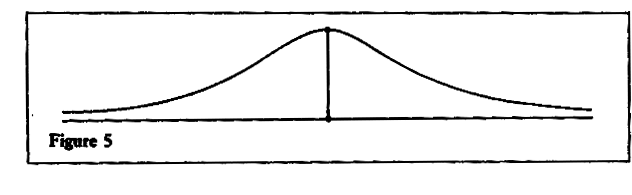
The value of the function never goes below 0 or above 1, and the denominator never vanishes. Despite this, we still hit trouble if we try x = 3: it gives the result
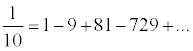
Although there are methods for testing when a series of real numbers makes good sense (that is, it is convergent), they involve quite a lot of calculation.
In contrast, if we look at this question from the point of view of complex numbers, there is a very simple test.
The corresponding complex function 
does have values
of z for which the denominator vanishes
(and the value becomes infinite), namely z
= i and z = - i. If we draw these
points in the complex plane, using (x,y) to represent x+iy as usual,
we get Figure 6. The points z =
± i, at which infinite values of the function occur, are its singularities.
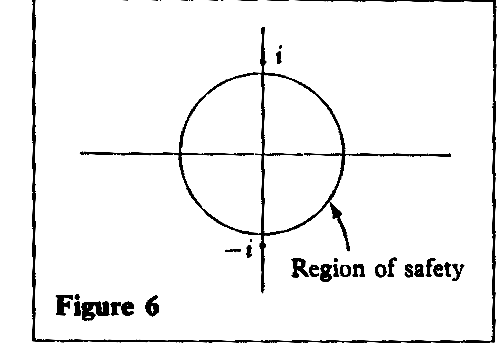
In the world of complex numbers there is a very simple test for convergence of a power series. Draw any circle, with its centre as the origin, that does not contain any singularity of the function. Then the series converges for all z inside that circle. If z is further from the origin than some singularity, then the series definitely does not converge for that value of z.
For we can take any circle of radius less than 1, but we expect problems of non-convergence outside the
circle of radius I. In particular, we expect trouble when z = 3. (Note that when z is real, then z =
x + i0 = x; its real part. So z = 3 is the point x =
3, y = 0.)
This is much more satisfying than some intricate calculation. It says that the series behaves badly because the
function it represents behaves badly. Indeed, much more is true. In general, infinite series have to be handled
very carefully. There are many things that look quite reasonable - changing the order of the terms, or differentiating
or integrating the series term by term - that can sometimes lead to incorrect conclusions. There is a blanket theorem,
which I have never seen stated in quite this way in any textbook:
Within a circle centred at the origin, not containing any singularity,
you can safely carry out any operation on the power series that might occur to a sane mathematics student.
Warwick Sawyer retired from the University of Toronto in 1976. Previously he taught mathematics at university level
in Britain, New Zealand and the USA. From 1948 to 1950 he was the first Head of Mathematics at the Universitv of
Ghana. He has written twelve books, including Mathematician's Delight and Prelude to Mathematics. Their aim is
to enable scientists, engineers and the general public to use any mathematics they might need, with understanding
and without anxiety.
This article first appeared in the November 1991 issue of Mathematical Review.
Copyright © W. W. Sawyer & Mark Alder 1991, 2001
Version: 22nd March 2001
|