[Home Page] The Work of W. W. Sawyer By David M. Clarkson Warwick Sawyer, who retired in June 1976 as Professor jointly to the Department of Mathematics and the College of Education, University of Toronto, has made a consistent and impressive contribution to mathematics education in the world for the past three decades. From the publication of his most successful book (continuously in print since 1943, ten translations, and about half a million copies Mathematician's Delight to his latest An Engineering Approach to Linear Algebra, in his numerous journal articles and speeches, and perhaps most importantly in his personal encouragement of students and teachers. Sawyer has exercised a profound effect on the teaching of mathematics in and out of schools. It is in some sense ironic that his consistency of view has sometimes placed him on the right wing and sometimes on the left of pedagogic controversy, for any rereading of his published work offers considerable evidence that his recommendations were based basic, perennial issues, carefully analyzed, and that his defense of them cannot properly be considered in the context of, say, the 'modern maths' wars of the 1960s. Indeed, the scope of Sawyer's contribution far exceeds curricular issues, and this is as evident in his first book as it is in his latest. As a mathematician, Sawyer is concerned to identify those aspects of mathematics that are most useful, and to emphasize these in establishing curricula. He defines 'useful' as that mathematics which is actually most used these days as well as those topics which are most likely to be of use in future. It is extremely difficult to define what the mathematical needs of society are, . . . yet it is something we ought to know. It is one of the criteria by which we have to judge what we are doing .... l was unwilling to say that the whole of modern mathematics was useless unless I had gone carefully through it and considered whether any parts it had use. . . I have tried to collect evidence . . . it is not at all easy . . Mathematicians tend to be uninterested in the engineering applications and ignorant of them. Engineers tend to be ignorant of mathematics since l900 ... I have looked through the 1962 volume of SIAM (Society for Industrial and Applied Mathematics) and in the first 350 pages of that, covering about 24 papers, I have tried to access the kind of mathematics being used . . . (Problems in Teaching Mathematics in Schools and Colleges and Universities.) Sawyer found that by this criterion, classical mathematics (in particular, calculus), vectors and matrices, and functional analysis were of the most use, in that order. He proposed that some way be found to inform the teaching profession of the mathematics currently most useful, as the list and its order were bound to change. This whole approach is typical of Sawyer's practicality when dealing with sticky issues. A second problem he addressed was the question of organization. The best way to learn geometry is to follow the road which the human race originally followed: Do things. make things, notice things, arrange things, and only then reason about things. (Mathematician's Delight., P. 17) His basic reason for this view sounds very Piagetian today ". . . education consists in co-operating with what is already inside a child's mind". (p.27). The genetic approach attends to this need; the logical approach; especially the axiomatic, ignores it. His books abound with specific examples of this philosophy. For instance, The Search for Pattern he rejects theca common method of introducing negative and fractional exponents in algebra courses so as to preserve the laws which hold for positive integral exponents on the grounds that such arguments are unconvincing to students, and, noting that Napier's invention of logs preceded Wallis's introduction of fractional and negative exponents by nearly half a century, proposes the early discussion of logarithms in the simple seventeen century manner. 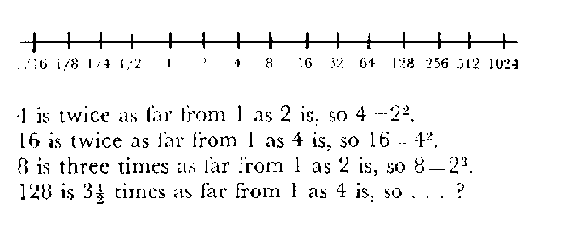It is then possible to use a logarithmic scale to explain fractional exponents as follows: Sawyers inventiveness in finding physical illustrations of basic concepts is nicely illustrated in Chapter 6 (How to forget the multiplication table) of M.D. where he considers the logarithmic effect of winding a rope around a post. Suppose that the rope and post are of such a size that one full turn has the holding power of ten times the pull on the other end; two full turns will then have holding power of 10 X 10 or 102, having thus given concrete meaning to such abstractions 108 (eight full turns of the rope about the post), he defines "the number of turns required to get any number" corresponding to your holding power as "the logarithm of the number". Since 102is the magnifying effect of two turns, 101/2 is that of half a turn and "the logarithm of 2 will be that fraction of a turn which is necessary to magnify your pull 2 times". This is certainly a far cry from traditional methods of introducing logarithms! The search for simple starting points, the essence of the genetic approach (since most mathematics starts from attempting to solve problems) was Sawyer's first and constant effort. Perhaps he was stimulated by his early teaching experiences. After a superior mathematics education at Highgate School (the Headmaster was a mathematician) he took his B.A. at St. John's College, Cambridge. But before assuming a lectureship at Dundee, Sawyer obtained permission from his old head to take some of the lowest classes at Highgate. I knew I should be doing something different, but I did not know what. The boys said they were interested in aeroplanes. It was only afterwards that I realised what opportunities I had missed, and how, beginning with this general interest. . . I could have led the class into various parts of mathematics. In a class I was taking there was one boy who was much older than the rest. He clearly had no motive to work. I told him that, if he could produce for me, accurately to scale, drawings of the pieces of wood required to make a desk like the one he was sitting at, I would try to persuade the Headmaster to let him do woodwork during the mathematics hours - in the course of which, no doubt, he would learn something about measurement and numbers. Next day, he turned up with this task completed to perfection. This I have often found with pupils; it is not so much that they cannot do the work, as that they see no purpose in it. (A European Education.) Sawyer was by no means alone in thinking of the usefulness of mathematics and a genetic approach in teaching it. During the height of the curricular controversy of the sixties the memorandum On the Mathematics Curriculum of the High School was signed by 55 leading North American mathematicians from a list of seventy-five invited to sign it, including such men as Garrett Birkhoff, Richard Courant, H. S. M. Coxeter, Marston Morse, George Polya and, of course, Sawyer, and asserted that "the introduction of new terms and concepts should be preceded by sufficient concrete preparation and followed by genuine, challenging applications . . .". One of Sawyer's biggest contributions to the "concrete", though evident in examples from Mathematicians Delight, cane as a result of his work as Head of Mathematics at Leicester College of Technology from 1945 to 1947. The Departmental study of applications of mathematics to industry resulted in construction of numerous mechanical models for instruction. Sawyer believes that much mathematical activity is a search for pattern, and that children often "fail to solve problems because they cannot understand what the problems are". (Vision, p.6) Hence much of Sawyer's writing and teaching is "based on the idea of the pupil discovering mathematics mathematics for himself". (Ibid.) In his writings for children (and their teachers) he makes extensive use of the rectangular array model for all kinds of multiplication, and introduces the basic algebraic concepts by a model, first used in M.D., of "pebbles in the bag". The influence of these approaches may be seen by the number of textbook writers who have incorporated them in their own work. Sawyer subsequently published a pamphlet of these devices, Math Patterns in Science, and they appear in most of his books, especially in Chapter 1 (Mathematics through the hand) of for The Search for Pattern. Nor was his concern limited to secondary school students or college students. As early as Mathematician's Delight he is writing of concrete models for simple arithmetic, and an experimental approach for juniors is outlined in an early book with L. G. Srawley, Designing and Making. Later, in America, he spent the 1958-9 academic year regularly teaching a class of l l-year-olds in a public elementary school in Middletown, Connecticut. The results of this experiment were collaboration with Bob Wirtz and Morton Botel (joined later by Max Beberman) in a new kind of elementary program entitled Math Workshop for Children, An overview of the philosophy behind this method is to be found in Vision in Elementary Mathematics as well as in numerous journal articles. On the secondary level, Sawyer emphasised elementary approaches to calculus, again based on work with children in the 12 to 15-year-old age range. First examples of this appear in Mathematician's Delight, especially Chapters 10-12, and later in What is Calculus About? He starts the discussion in M.D with - "The Basic Problem". The basic problem of differential calculus is the following: we are given a rule for finding where an object is at any time, and are asked to find out how fast it is moving. (p. 12l) This definition of the "The Basic Problem" is repugnant to those mathematicians who want to start with what Sawyer called "the analysis or epsilon-delta stage" (What is Calculus About?, p108) but is consistent with Sawyer's genetic approach. During the years 1600-1800 A.D. calculus was concerned with very much the kind of problems, and used very much the kind of thinking, that you have seen in this book. Then, gradually, a crisis developed. (Op. cit. p. 93) The results of the crisis created a calculus that was more rigorous but also more difficult to learn, and perhaps not everyone needs to begin "with the latest and most fashionable model" (p.94). So, Sawyer's first approach has always been intuitive. For example in M.D. he considers the problem of finding y' corresponding to the formula y = log x by use of the method of "rough ideas". By By filling out a table of values from x (holding power) = 1 to 10, with the corresponding columns for y= log v (parts of a full turn), Dy, and Dy/Dx, he leads the reader to form the conjecture, by pattern, that "y" corresponding to y=log x is something like 0.414/x. The inconvenience of 0.411- motivates discussion of natural logs, and leads to the result that if y=logex, then y=1/x. But he does not just stop with the intuitive approach. What is Calculus About? ends with a Guide to further study. Asserting that it is extremely important to read books about calculus in the correct order, he outlines a progression that starts with Durell and Robson's Elementary Calculus, through Klein to Courant's Differential and Integral Calculus, and a variety of texts for those with special interests. His elementary university level work has been mainly in the field of linear algebra, starting with the general Prelude to Mathematics, and A Concrete Approach to Abstract Algebra which was an outgrowth of the course he taught for secondary school teachers at the University of Illinois in 1957. The article Algebra contained more ideas, and was followed by another general work, A Path to Modern Mathematics, and finally his latest, a textbook for first year university students, An Engineering Approach to Linear Algebra. This last book is a very carefully thought out course, developed with his classes at Toronto during 1970-72, and perhaps represents Sawyer's methods at their best. In the preface, Sawyer says that "the student learns to picture or imagine the things he is dealing with, and then, because his imagination is working, he is able to reason about these things". Opposed to the lecture method of instruction as technologically backward, Sawyer uses a text as something for students to read, and the classes as opportunities to argue about the meanings of what has been read. When we speak, we improvise. When we write, we examine what we have written and amend it many times until it expresses truly what we wish to say. (Ibid.) For those who wish to assess Sawyer's written contribution to mathematics education, this book is probably the canonical form. One hopes, of course, that in his retirement more books are forthcoming, for instance the missing Volume 2 of Introducing Mathematics, or a more complete library of his mechanical devices. But Sawyer's contributions are by no means exhausted by the printed word. As much as any major figure in mathematics education over the past three decades he has exerted a personal influence on students and teachers worldwide. After establishing a Mathematics Department at University College, (Gold Coast (now University of Ghana) in 1948-50, he went to Canterbury College in New Zealand for five years, 1951-56, the University of Illinois in 1957-8, Wesleyan University for seven, 1958-65, before settling down at Toronto in 1965. In each of these places he was confronted with hard new problems which he addressed with his usual practical methods, What kind of mathematics do bright young students of a developing country with no mathematics traditions need? (Ghana) How can the supply of good mathematics teachers be improved? (New Zealand) What curriculum for high schools? (Illinois) Problem solving in industry and government for bright university undergraduates (Wesleyan) and mobilising elementary school teachers in Canada to provide concrete experiences for their children in the late sixties; these were a few of Sawyer's crusades over the years. In each case, the attempts at solutions were practical. Where do teachers form their attitudes towards mathematics? In schools. How do you improve teaching? Work on the teachers before they become teachers. But students enter Training College with a clear (and usually unshakable) idea of what schooling is - it is what they have themselves experienced as pupils. If a student has gone to a poor high school, the university is his last chance of actually experiencing good teaching as a pupil. To make a change, something must be done while the student is still suffering instruction. (A European Education, p. 26) But, Sawyer noted, even at the university level "resources both of manpower and of finance" were extremely limited. We had [in New Zealand] the choice of trying to organize teachers, university students, high school pupils, or grade school pupils. The most spectacular results could undoubtedly have been obtained with grade school children. But there were so many grade schools, and it would have been many years before these children could become teachers. It was accordingly decided to make an attempt at high school level. (Op. Cit. p. 27) The essential quality for a mathematician is the habit of thinking things out for oneself. That habit is usually acquired in childhood. It is hard to acquire it later. (Ibid.) So, with backing from Canterbury College, Sawyer established a mathematics club for sixth form pupils in 1952. It ran for the six years he was there, and after, with a steady attendance of 100 to 150 enthusiastic members. We settled into the custom of having two challenge meetings and four lectures each year. . . . The papers set by pupils tended to contain some problems that were harder than anyone on the faculty set. . . . Having to present and explain solutions to a large audience was all excellent training for pupils who might later become teachers. One very interesting thing thing happened, which I knew nothing about until years later. In one of the girl's schools, the teachers waited until the girls had solved all the problems they were able to. They then arranged for the girls in the society, who were juniors or seniors, to explain the problems and solutions to the sophomores. The girls would give what they thought was a very clear explanation. At the end, they would find the sophomores had not understood a word of it, So they would try again and would continue until they had found a way of explaining the work that was understood by the sophomores. After this experience of presenting the solution to pupils a year or two younger than themselves, they came to the meeting of their contemporaries with explanations that were extremely clear. (Ibid., p, 3 l) One boy, of very high ability, gave a most thorough and scholarly report on number theory, which the members of the society were able to understand. After the talk, I learned that the members from the Girl's High School had threatened to walk out in a body, if he said anything they could not understand. He had given his talk under the menace of this threat . . . (p. 33) There are some professors of mathematics who might have benefited from this treatment, had it been administered to them in their youth. A teacher was only invited to talk to the society if we had an assurance from the pupils of his school that this teacher was lively and inspiring . . . In this way, pupils came to accept as normal what was in fact exceptional. They began to picture what a mathematical lesson could and should be, in terms of what was done by the best teachers in the most fortunate schools. (p. 37) The club was clearly a successful effort as far as its members were concerned, and there is even some evidence that it may have had an effect on teacher recruitment. Statement by Mr. Gordon Troup. liason officer between Canterbury University College and the schools, November 1956: While it is no part of my duties to solicit recruits for any particular vocation, it does lie within my province to note down objectively what professions the sixth-formers of Canterbury and Westland intend to pursue, and to observe with what success or otherwise they subsequently pursue them. And there can be no doubt that the recruitment of teachers of mathematics at this time is critical, in every sense of the word. My observations cover a period of thirteen years. and there is a very distinct watershed at 1950. which coincides with the foundation of this very remarkable Sixth Form Mathematical Society. And the figures I am going to quote indicate that some strong, new influence came to bear on maths teaching vocations just at that time. In the five years from 1946 to l950 inclusive, the Sixth Forms mathematics class rolls increased steadily from 295 to 300, with a mean of 295 or 300. During that period 6 pupils announced their intention of taking up maths teaching. In the following five years, the mean increase [of the class rolls] was about 66 per cent. In the same period, the declared mathematical teaching vocations were 19, an increase of over 200 per cent... (Op cit., p. 39) In the States, as Editor of the Mathematics Student Journal (N.C.T.M.), he solicited articles and problems from high school students, and contrary to the general expectation of the time, whole issues were entirely written by students before his two years as editor were up (November 1958-May 1961). Teacher training? Go into the schools and work with teachers. As editor (with L.D Nelson) of MATHEX, Sawyer solicited a wide range of contributions from elementary school classroom teachers. At one point he proposed a novel method of teacher training. . . . go into a street or park or public place where there are children over whom you have no disciplinary powers, and start doing something to sec how many children come round you, how long they stay. and what questions they ask. (Mathematics in Secondary Schools.) Perhaps Sawyer's most important contribution to mathematics education as whole is his encouragement of individuals to try out new ideas and "buck the system if necessary". He did not just say "Once more into the breach" and let it go at that. On many occasions he followed through with attempts to enlist support for an innovative teacher from administrators. Sawyer has always been willing to offer his personal services, free, to such causes, and takes pains to endorse individuals by name in his articles and speeches. One can expect that he will not retire from these activities. Recently, David Wheeler called on mathematics educators to "develop criteria . . . which will give everyone concerned with decisions, the tools for making better judgments" (MT No. 75). Sawyer devoted his professional career to asking, and attempting to form criteria for, such difficult questions as: What mathematics is important to teach? How can the curriculum be best organised? What methods work, and when, and with whom? There is no necessity to agree with his criteria, although the evidence in support of them is often impressive, but the continual asking of the questions is vital. Re-read Sawyer; he was never more relevant than today! References. Books Mathematics Delight (Penguin 1943) Mathematics in Theory and Practice (Odhams 1948) (edited by Sawyer, who wrote six of the ten chapters) Prelude to Mathematics (Penguin 1955) Designing and Making (with L. G. Srawley) (Blackwell 1957) A Concrete Approach to Abstract Algebra (W. H. Freeman 1959) Maths Patterns in Science (American Education Publications, 1960) What is Calculus About? ( New Mathematical Library, S.M.S.G., Yale l 960) Introducing Mathematics: 1 Vision in Elementary Mathematics (Penguin 1964) reviewed in MT No. 28). Introducing Mathematics: 4 A Path to Modern Mathematics (Penguin 1966) reviewed in MT No. 38) Maths Workshop,a worktext for children (with teacher's guides) Levels A-F, with Wirtz, Botel and Beberman. (Encyclopaedia Britannica Press, Chicago,.Toronto 1962: revised 1967) (reviewed in MT No 27) Introducing Mathematics: 3 The Search for Pattern (Penguin 1970) reviewed in MT No. 33) An Engineering Approach to Abstract Algebra (Cambridge, 1972) Editorships The Mathematics Student Journal (N.C.T.M., Vol 6 No 1, November 1958 to Vol 8 No. 4, May 1961) MATHEX; Teacher's Resource Books, Gen Ed. with L. D. Nelson (E. B. Press, Montreal 1970) Articles Things and Un-Things (The Mathematics Teacher (TMT), Jan 1958 Plans for the Journal (TMT. Feb. 1958) The Possibility of Universal Mathematical Literacy (New York State Mathematics Teachers Journal, October 1958) Open Letter to Dr. Joseph Seidlin, (NYSMTJ, Jan 1959) Why is Arithmetic Not the End? (The Arithmetic Teacher, N.C.T.M.., March March 1959) The Concrete Basis of the Abstract (TMT, Apr. 1959) Proofs with a New Format (TMT, Oct. 1959) The Reconstruction of Mathematical Education (Journal of Engineering Education, Nov. 1960) By David M. Clarkson A. Y. Jackson Secondary School Willowdale, Ontario Canada This article first appeared in the December 1976 issue (p 51-54) of Mathematics Teaching published by The Association of Teachers of Mathematics. email: atm_maths@compuserve.com We are grateful for the permission of the Association to reproduce the above article. Copyright © W. W. Sawyer & Mark Alder 2000 Version: 28th April 2001 Back [Home Page]